题目内容
如果ab=-1，那么w=
的取值范围是（ ）
| a2-b2 |
| a+b |
| A．（-∞，-2）∪（2，+∞） | B．（-∞，-2]∪[2，+∞） | C．（-2，2） | D．[-2，2] |
∵ab=-1∴b=-
∴w=
=a-b=a+
要使上式有意义a≠±1
当a＞0时，a+
≥2
=2，等号取不到；
当a＜0时，a+
=-（-a-
）≤-2
=-2，等号取不到；
综上所述w的范围是（-∞，-2）∪（2，+∞）
故选A．
| 1 |
| a |
∴w=
| a2-b2 |
| a+b |
| 1 |
| a |
要使上式有意义a≠±1
当a＞0时，a+
| 1 |
| a |
a•
|
当a＜0时，a+
| 1 |
| a |
| 1 |
| a |
(-a)•(-
|
综上所述w的范围是（-∞，-2）∪（2，+∞）
故选A．
练习册系列答案
相关题目
直线l过点（-4，0）且与圆（x+1）2+（y-2）2=25交于A、B两点，如果|AB|=8，那么直线l的方程为（ ）
| A、5x+12y+20=0 | B、5x-12y+20=0或x+4=0 | C、5x-12y+20=0 | D、5x+12y+20=0或x+4=0 |
如果ab=-1，那么w=
的取值范围是（ ）
| a2-b2 |
| a+b |
| A、（-∞，-2）∪（2，+∞） |
| B、（-∞，-2]∪[2，+∞） |
| C、（-2，2） |
| D、[-2，2] |
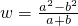的取值范围是
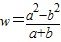的取值范围是（ ）