题目内容
已知函数![]()
(I)讨论函数f(x)单调性;
(Ⅱ)当![]() 时,证明:曲线
时,证明:曲线![]() 与其在点
与其在点![]() 处的切线至少有两个不同的公共点.
处的切线至少有两个不同的公共点.
解:
(Ⅰ)f(x)的定义域为(0,+∞),f¢(x)=2ax-![]() .
.
(1)若a≤0,则f¢(x)<0,f(x)在(0,+∞)是减函数; …2分
(2)若a>0,则当x∈(0,![]() )时,f¢(x)<0,f(x)在(0,
)时,f¢(x)<0,f(x)在(0,![]() )是减函数;
)是减函数;
当x∈(![]() ,+∞)
,+∞)![]() 时,f¢(x)>0,f(x)在(
时,f¢(x)>0,f(x)在(![]() ,+∞)是增函数. …4分
,+∞)是增函数. …4分

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
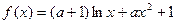
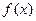 的单调性;
的单调性;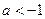 .如果对任意
.如果对任意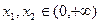 ,
,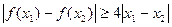 ,求
,求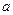 的取值范围。
的取值范围。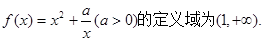
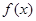 在其定义域上的单调性;
在其定义域上的单调性;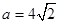 时,若关于x的方程
时,若关于x的方程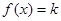 恰有两个不等实根,求实数k的取值范围。
恰有两个不等实根,求实数k的取值范围。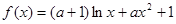
 的单调性;
的单调性;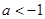 .如果对任意
.如果对任意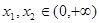 ,
,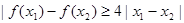 ,求
,求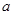 的取值范围。
的取值范围。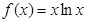
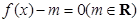 的解的个数;
的解的个数;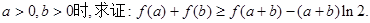
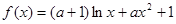
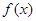 的单调性;
的单调性;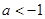 .如果对任意
.如果对任意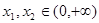 ,
,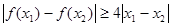 ,求
,求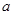 的取值范围。
的取值范围。