题目内容
已知函数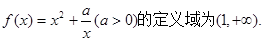
(I)讨论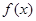 在其定义域上的单调性;
在其定义域上的单调性;
(II)当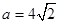 时,若关于x的方程
时,若关于x的方程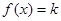 恰有两个不等实根,求实数k的取值范围。
恰有两个不等实根,求实数k的取值范围。
【答案】
(Ⅰ)1)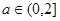 时,
时,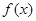 在
在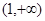 单调递增; 2)
单调递增; 2)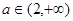 时,
时,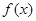 在
在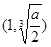 单调递减;
单调递减;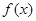 在
在 单调递增. (Ⅱ)
单调递增. (Ⅱ)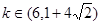
【解析】本试题主要是考查了导数在研究函数中的运用,通过导数与函数单调性的关系的研究得到函数的最值,并从而研究函数与方程的问题的综合试题。
(1)对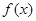 求导得然后分析根与定义域的位置关系来判定函数的单调性。
求导得然后分析根与定义域的位置关系来判定函数的单调性。
(2)要分析方程根的问题,可以转化为图像与图像的交点问题来解决。
解:(Ⅰ)对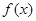 求导得:
求导得: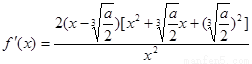 ;……2分
;……2分
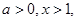 则显然有
则显然有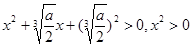
当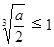 时,即
时,即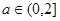 ,
,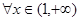 时,
时,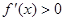 ,则:
,则: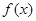 在
在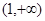 单调递增;
单调递增;
当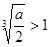 时,即
时,即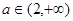 ;当
;当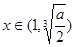 时,
时,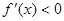 ,则
,则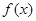 在
在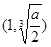 单调递减;
单调递减;
当 时,
时,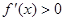 ,则
,则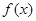 在
在 单调递增;
单调递增;
综上可知:1)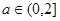 时,
时,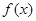 在
在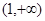 单调递增;
单调递增;
2)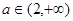 时,
时,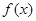 在
在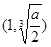 单调递减;
单调递减;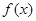 在
在 单调递增.……6分
单调递增.……6分
(Ⅱ)当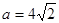 时,由(Ⅰ)可知:
时,由(Ⅰ)可知: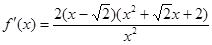 ;于是:
;于是:
当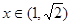 时,
时,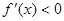 ,则:
,则: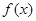 在
在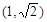 单调递减;
单调递减;
当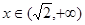 时,
时,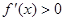 ,则:
,则: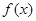 在
在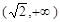 单调递增;
单调递增;
当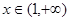 时,
时,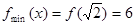 ,
,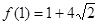 ,
, 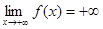 ;
;
欲使方程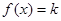 恰有两个不等实根,则有:
恰有两个不等实根,则有: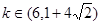

练习册系列答案
相关题目
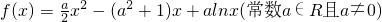
 与a的大小.
与a的大小.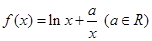
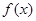 的单调性;
的单调性;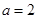 时,求函数
时,求函数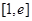 上的最值.
上的最值.