题目内容
P为矩形ABCD所在平面外一点，且PA⊥平面ABCD，P到B，C，D三点的距离分别是
，
，
，则P到A点的距离是（ ）
| 5 |
| 17 |
| 13 |
分析：由题意画出图形，利用题目给出的已知条件得到及格直角三角形，设出PA的长度x，然后在直角三角形中利用勾股定理列式求解x的值．
解答：
解：如图，
设AB=a，BC=b，PA=x．
因为PA⊥平面ABCD，所以△PAB，△PAC，△PAD均为Rt△．
又底面为矩形，所以△ABC也为Rt△．
再由PB=
，PC=
，PD=
．
得：
，解得：x=1．
所以P到A点的距离为1．
故选A．
解：如图，设AB=a，BC=b，PA=x．
因为PA⊥平面ABCD，所以△PAB，△PAC，△PAD均为Rt△．
又底面为矩形，所以△ABC也为Rt△．
再由PB=
| 5 |
| 17 |
| 13 |
得：
|
所以P到A点的距离为1．
故选A．
点评：本题考查了点线面间的距离的计算，考查了学生的空间想象能力和计算能力，是中档题．
练习册系列答案
相关题目
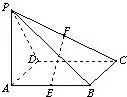17、如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E、F分别为AB、PC的中点．
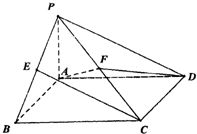如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E，F分别为线段PB，PC的中点，且AD=4，PA=AB=2