题目内容
P为矩形ABCD所在平面外一点，且PA⊥平面ABCD，P到B，C，D三点的距离分别是
，
，
，则P到A点的距离是
| 5 |
| 17 |
| 13 |
1
1
．分析：根据线面垂直的判定与性质，证出△PAB、△PAD、△PBC都是直角三角形．因此设PA=x，AB=y且AD=z，结合题中数据建立关于x、y、z的方程组，解之得到x、y、z的值，即可得到P到A点的距离．
解答：解：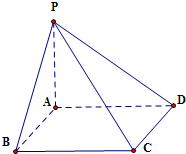
设P到A点的距离PA=x，AB=y且AD=z，则
∵PA⊥平面ABCD，AB、AD、BC?平面ABCD，
∴PA⊥AB，PA⊥AD，PA⊥BC
∵BC⊥AB，AB∩PA=A，
∴BC⊥平面PAB，可得BC⊥PB
Rt△PAB中，PB=
=
…①
同理，可得PD=
=
…②，PC=
=
…③
将①②③联解，可得x=1，y=2，z=3
故P到A点的距离PA=1
故答案为：1
设P到A点的距离PA=x，AB=y且AD=z，则∵PA⊥平面ABCD，AB、AD、BC?平面ABCD，
∴PA⊥AB，PA⊥AD，PA⊥BC
∵BC⊥AB，AB∩PA=A，
∴BC⊥平面PAB，可得BC⊥PB
Rt△PAB中，PB=
| x2+y2 |
| 5 |
同理，可得PD=
| y2+z2 |
| 13 |
| x2+y2+z2 |
| 17 |
将①②③联解，可得x=1，y=2，z=3
故P到A点的距离PA=1
故答案为：1
点评：本题给出四棱锥的底面为矩形且一条侧棱与底面垂直，在已知三条斜侧棱的情况下求四棱锥的高．着重考查了线面垂直的判定与性质、勾股定理与空间距离的求法等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
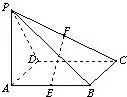17、如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E、F分别为AB、PC的中点．
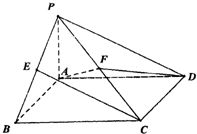如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E，F分别为线段PB，PC的中点，且AD=4，PA=AB=2