题目内容
P为矩形ABCD所在平面外一点，且PA⊥平面ABCD，PB=2
，PC=
，PD=
，则四棱锥P-ABCD的体积等于（ ）
| 2 |
| 17 |
| 13 |
分析：作出图象设AB=a，AD=b，由勾股定理可得a=2，b=3，PA=2四棱锥P-ABCD的体积V=
×2×3×2=4，可得答案．
| 1 |
| 3 |
解答：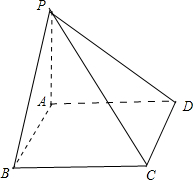
解：由题意作出图象，设AB=a，AD=b，在直角三角形PAB、PAD、PAC中，由勾股定理可得，
PA2=(2
)2-a2=(
)2-b2=(
)2-(a2+b2)，解得，a=2，b=3，PA=2，
所以四棱锥P-ABCD的体积V=
×2×3×2=4，
故选B．
解：由题意作出图象，设AB=a，AD=b，在直角三角形PAB、PAD、PAC中，由勾股定理可得，PA2=(2
| 2 |
| 13 |
| 17 |
所以四棱锥P-ABCD的体积V=
| 1 |
| 3 |
故选B．
点评：本题为四棱锥体积的求解，关键是作出图象，通过设未知量，利用勾股定理解出用到的长度，属基础题．
练习册系列答案
相关题目
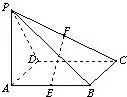17、如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E、F分别为AB、PC的中点．
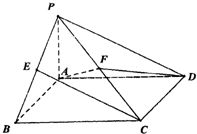如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E，F分别为线段PB，PC的中点，且AD=4，PA=AB=2