题目内容
函数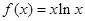 的单调递增区间是________________.
的单调递增区间是________________.
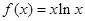 的单调递增区间是________________.
的单调递增区间是________________.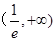
试题分析:求
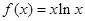 的导数f’(x),由f’(x)>0,即可求得答案。解:∵f’(x)=lnx+1,令f’(x)>0得:lnx>-1,∴x>e-1=
的导数f’(x),由f’(x)>0,即可求得答案。解:∵f’(x)=lnx+1,令f’(x)>0得:lnx>-1,∴x>e-1=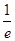 .∴函数
.∴函数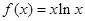 的单调递增区间为(
的单调递增区间为(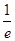 ,+∞).故填写
,+∞).故填写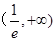 。
。点评:本题考查利用导数研究函数的单调性,易错点在于忽视函数的定义域,属于中档题.

练习册系列答案
相关题目
题目内容
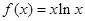 的单调递增区间是________________.
的单调递增区间是________________.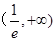
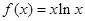 的导数f’(x),由f’(x)>0,即可求得答案。解:∵f’(x)=lnx+1,令f’(x)>0得:lnx>-1,∴x>e-1=
的导数f’(x),由f’(x)>0,即可求得答案。解:∵f’(x)=lnx+1,令f’(x)>0得:lnx>-1,∴x>e-1=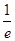 .∴函数
.∴函数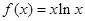 的单调递增区间为(
的单调递增区间为(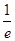 ,+∞).故填写
,+∞).故填写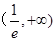 。
。