题目内容
【题目】已知函数
，
.
（1）设函数
，讨论
的极值点个数，并求出相应极值；
（2）若
，且
，求证：
.
【答案】（1）极值点个数见解析，相应极值见解析；（2）证明见解析
【解析】
（1）求出
的导函数，对a进行分类讨论求解讨论极值点；
（2）根据导函数得
，结合
在
上单调递增，即可得证.
（1）函数
，
∴
，
令
，解得
或
，
当
时，
；当
时，
.
①若
时，在
上单调递增，在
上单调递减，
在
上单调递增，有2个极值点.
∴当时，函数有极小值，极小值为
；
当时，函数有极大值，极大值为
.
②当
时，在
上单调递增，
在
上单调递减，在
上单调递增，有2个极值点，
∴当时，函数有极大值，极大值为；
当时，函数有极小值，极小值为.
③当
时，
，
∴在R上单调递增，无极值点，故无极值.
（2）∵
，
又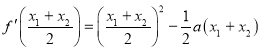
，
∴，
又
在上单调递增，
∴
时，有
，
∴
.
【题目】甲、乙两人在相同条件下各射击
次，每次中靶环数情况如图所示：
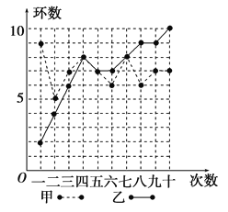
（1）请填写下表（先写出计算过程再填表）：
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
（2）从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看（分析谁的成绩更稳定）；
②从平均数和命中
环及环以上的次数相结合看（分析谁的成绩好些）；
③从折线图上两人射击命中环数的走势看（分析谁更有潜力）.
参考公式：
.
【题目】为了研究某学科成绩是否与学生性别有关，采用分层抽样的方法，从高三年级抽取了30名男生和20名女生的该学科成绩，得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图，规定80分以上为优分（含80分）．
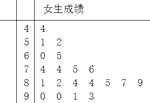
（Ⅰ）（i）请根据图示，将2×2列联表补充完整；
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
（ii）据此列联表判断，能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”？
（Ⅱ）将频率视作概率，从高三年级该学科成绩中任意抽取3名学生的成绩，求至少2名学生的成绩为优分的概率．
附：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
．
