题目内容
12.若n∈N*,则$\sqrt{{4}^{-n}+{2}^{1-n}+1}$+$\sqrt{{4}^{-n}-{2}^{1-n}+1}$=( )| A. | 2 | B. | 2-n | C. | 21-n | D. | 2-2n |
分析 直接把根式内部的代数式化为完全平方的形式得答案.
解答 解:$\sqrt{{4}^{-n}+{2}^{1-n}+1}$+$\sqrt{{4}^{-n}-{2}^{1-n}+1}$
=$\sqrt{({2}^{-n})^{2}+2•{2}^{-n}+1}$$+\sqrt{({2}^{-n})^{2}-2•{2}^{-n}+1}$
=$\sqrt{({2}^{-n}+1)^{2}}+\sqrt{({2}^{-n}-1)^{2}}$
=2-n+1+1-2-n=2.
故选:A.
点评 本题考查根式与分数指数幂的互化,考查了有理指数幂的化简与求值,是基础题.

练习册系列答案
相关题目
3.函数f(x)=$\frac{{(x+1)}^{0}}{\sqrt{|x|-x}}$的定义域是 ( )
| A. | (-∞,0)∪(0,1) | B. | (-∞,-1)∪(-1,0) | C. | (-1,0)∪(0,+∞) | D. | [-1,0)∪(0,+∞) |
17.已知函数y=$\frac{{x}^{2}}{2}$的定义域为[-2,2],则y=f(x)的值域为( )
| A. | [-1,1] | B. | [1,2] | C. | [0,2] | D. | [0,3] |
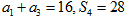
 取何值时Sn最大,并求出这个最大值
取何值时Sn最大,并求出这个最大值