题目内容
在正三棱锥P-ABC中,M,N分别是PB,PC的中点,若截面AMN⊥侧面PBC,则此棱锥截面与底面所成的二面角正弦值是
.
| ||
| 6 |
| ||
| 6 |
分析:取MN和BC的中点分别为E,F,可以证明BC∥截面AMN,设截面AMN∩平面ABC=l,从而BC∥l,故可知∠EAF为所作的二面角,从而可求棱锥截面与底面所成的二面角正弦值.
解答: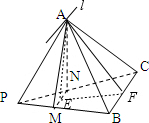 解:取MN和BC的中点分别为E,F,
解:取MN和BC的中点分别为E,F,
∵M,N分别是PB,PC的中点,
∴MN∥BC
∵MN?截面AMN
∴BC∥截面AMN
设截面AMN∩平面ABC=l
∴BC∥l
∵E,F分别为MN和BC的中点
∴AE⊥MN,AF⊥BC
∴∠EAF为所作的二面角的平面角,
设AB=a,∵截面AMN⊥侧面PBC,∴侧棱PA=PB=PC=
a,∴DF=
a,∴EF=
a
在直角△AEF中,AF=
a,EF=
a
∴sin∠EAF=
故答案为:
 解:取MN和BC的中点分别为E,F,
解:取MN和BC的中点分别为E,F,∵M,N分别是PB,PC的中点,
∴MN∥BC
∵MN?截面AMN
∴BC∥截面AMN
设截面AMN∩平面ABC=l
∴BC∥l
∵E,F分别为MN和BC的中点
∴AE⊥MN,AF⊥BC
∴∠EAF为所作的二面角的平面角,
设AB=a,∵截面AMN⊥侧面PBC,∴侧棱PA=PB=PC=
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
在直角△AEF中,AF=
| ||
| 2 |
| ||
| 4 |
∴sin∠EAF=
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题考查二面角的作法与计算,解题的关键是正确作出面面角、

练习册系列答案
相关题目
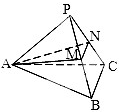 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|