题目内容
在正三棱锥P-ABC中,AB=
,PA=
+1,过点A作截面交PB,PC分别于D,E,则截面△ADE的周长的最小值是
+
+
.
| 2 |
| 3 |
| 6 |
| 2 |
| 6 |
| 2 |
分析:画出正三棱锥P-ABC侧面展开图,将问题转化为求平面上两点间的距离最小值问题,求出∠APB与∠APA1,即可求得结果.
解答: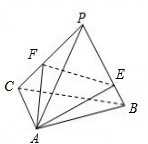
 解:三棱锥的侧面展开图,如图,
解:三棱锥的侧面展开图,如图,
△ADE的周长的最小值为AA1,
在△PAB中,sin
∠APB=
=
,∴
∠APB=15°,
∠APB=30°,
在△APA1中,∴sin∠APA1=sin90°=1,
所以AA1=
PA=
+
,
故答案为:
+
.

 解:三棱锥的侧面展开图,如图,
解:三棱锥的侧面展开图,如图,△ADE的周长的最小值为AA1,
在△PAB中,sin
| 1 |
| 2 |
| ||||
|
| ||||
| 4 |
| 1 |
| 2 |
∠APB=30°,
在△APA1中,∴sin∠APA1=sin90°=1,
所以AA1=
| 2 |
| 6 |
| 2 |
故答案为:
| 6 |
| 2 |
点评:本题考查的知识点是棱锥的结构特征,其中将三棱锥的侧面展开,将空间问题转化为平面上两点之间的距离问题,是解答本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
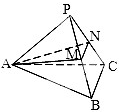 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|