题目内容
4、在正三棱锥P-ABC中,D、E分别是AB、BC的中点,有下列四个论断:①AC⊥PB;②AC∥平面PDE;③AB⊥平面PDE;④平面PDE⊥平面ABC.其中正确的个数为( )
分析:对于①利用正三棱锥的性质即可判定,对于②利用线面平行的判定定理进行判定,对于③利用反证法进行判定,对于④根据面面垂直的判定定理可判定.
解答: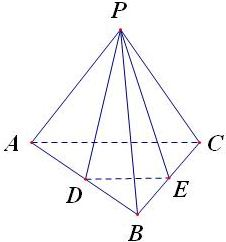 解:
解:
①根据正三棱锥的性质可知对棱互相垂直,故正确
②∵AC∥DE,AC?面PDE,DE?面PDE∴AC∥平面PDE,故正确
③若AB⊥平面PDE,则AB⊥DE,显然不正确
④点P在底面的投影是正三角形的中心,而此中心不在直线DE上,故平面PDE与平面ABC不垂直,故不正确
故选B
 解:
解:①根据正三棱锥的性质可知对棱互相垂直,故正确
②∵AC∥DE,AC?面PDE,DE?面PDE∴AC∥平面PDE,故正确
③若AB⊥平面PDE,则AB⊥DE,显然不正确
④点P在底面的投影是正三角形的中心,而此中心不在直线DE上,故平面PDE与平面ABC不垂直,故不正确
故选B
点评:本题主要考查了直线与平面平行的判定,以及直线与平面垂直的判定和平面与平面垂直的判定,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
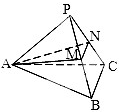 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|