题目内容
【题目】如图,CA,CB分别与圆O切于A,B两点,AE是直径,OF平分∠BOE交CB的延长线于F,BD∥AC. 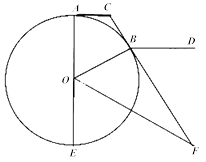
(1)证明:OB2=BCBF;
(2)证明:∠DBF=∠AOB.
【答案】
(1)证明:连接OC,由CA,CB为切线,可得CA=CB,
OA=OB,OC=OC,
即有△OAC≌△OBC,
即有∠AOC=∠BOC,
又OF平分∠BOE交CB的延长线于F,
可得∠EOF=∠BOF,
则∠FOC=∠FOB+∠BOC=∠EOF+∠AOC=90°,
在直角三角形COF中,OB为斜边CF上的高,
由射影定理,可得OB2=BCBF

(2)证明:由∠CAO=∠CBO=90°,可得
四点C,A,O,B共圆,延长AC至M,
即有∠MCB=∠AOB,
由BD∥AC,可得∠DBF=∠MCB,
即有∠DBF=∠AOB
【解析】(1)连接OC,运用切线的性质,可得△OAC≌△OBC,结合内角平分线的定义,可得∠FOC=90°,由直角三角形的射影定理,即可得证;(2)由对角互补,可得四点C,A,O,B共圆,延长AC至M,运用两直线平行的性质,即可得证.

练习册系列答案
相关题目