Question

如图,直三棱柱ABC—A₁B₁C₁中,AB=AC,AA₁=2AB,∠BAC=90°.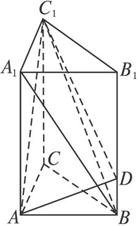

(1)在侧棱BB₁上找一点D,使得BC₁⊥AD,并说明理由;

(2)若点D满足条件(1),求二面角A-DC₁-C的大小.

Answer 1

解:(1)D点满足4BD=BB₁.

证明如下:连接BA₁,∵ABC—A₁B₁C₁是直三棱柱,∴面A₁B₁C₁⊥面ABB₁A₁.

又∵∠BAC=90°,∴C₁A₁⊥A₁B₁.∴C₁A₁⊥面ABB₁A₁.∴C₁A₁⊥BA₁.

由AA₁=2AB,4BD=BB₁得=2.

∴△A₁AB∽△ABD.∴AD⊥A₁B.又∵A₁B∩A₁C₁=A₁,∴AD⊥面A₁BC₁.∴BC₁⊥AD.

由以上证明可知D点唯一存在.(注:也可以用三垂线定理证明.)

(2)过A作AO⊥BC于O,∵ABC—A₁B₁C₁是直三棱柱,∴AO⊥面BCC₁B₁.

设AB=a,可得AO=a,

过O作OE⊥DC₁于E,连接AE,由三垂线定理可得∠AEO为二面角ADC₁C的平面角,

连接OC₁、OD,

∵=-S_△BOD--=2aaaa=a=×DC₁×OE=a×OE,∴OE=a.

∴tan∠AEO=.∴二面角A-DC₁-C的大小为arctan.