题目内容
【题目】如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
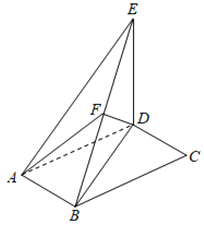
(1)求证:AB⊥DE;
(2)若点F为BE的中点,求直线AF与平面ADE所成角的正弦值.
【答案】(1)证明见解析(2)![]()
![]()
【解析】
(1)由已知结合余弦定理,求得![]() ,再由勾股定理的逆定理有ED⊥DB,根据面面垂直的性质定理可得ED⊥平面ABD,即可证明结论;
,再由勾股定理的逆定理有ED⊥DB,根据面面垂直的性质定理可得ED⊥平面ABD,即可证明结论;
(2)建立空间直角坐标系,求出![]() ,进而求出
,进而求出![]() 坐标和平面ADE法向量的坐标,按照空间线面角公式,即可求解.
坐标和平面ADE法向量的坐标,按照空间线面角公式,即可求解.
(1)在△ABD中,由余弦定理:
BD2=AB2+AD2﹣2ABADcos∠DAB,∴![]() ,
,
∴△ABD和△EBD为直角三角形,此即ED⊥DB,
而DB又是平面EBD和平面ABD的交线,
且平面EBD⊥平面ABD,ED平面EBD,
∴ED⊥平面ABD,AB平面ABD,∴AB⊥DE;
(2)由(1)知∠ABD=∠CDB=90°,以D为坐标原点,
DB,DC,DE所在的直线分别为x,y,z轴建立空间直角坐标系,
则![]() ,
,
则![]() ,设平面ADE的法向量为
,设平面ADE的法向量为![]() ,
,
则有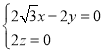 ,令x=1,则
,令x=1,则![]() ,
,
![]() ,设直线AF与平面ADE所成角为α,则有
,设直线AF与平面ADE所成角为α,则有![]() ,
,
所以直线直线AF与平面ADE所成角的正弦为![]() .
.


练习册系列答案
相关题目
【题目】十二生肖的座位次序如下图1,中间的狗、猪位置固定不动,其他生肖动物每次顺时针转动一格,即第一次转动后的座位次序如下图2,这样继续进行下去,那么第2019次换座位后,鼠的座位对应的编号为________.
图一:
鼠1 | 牛2 | 虎3 | 兔4 |
鸡10 | 狗11 | 猪12 | 龙5 |
猴9 | 羊8 | 马7 | 蛇6 |
图二:
鸡1 | 鼠2 | 牛3 | 虎4 |
猴10 | 狗11 | 猪12 | 兔5 |
羊9 | 马8 | 蛇7 | 龙6 |