题目内容
【题目】[选修4-4：坐标系与参数方程]
在直角坐标系
中，曲线
的参数方程为
（
为参数），直线
的方程为
．
（1）以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，求曲线的极坐标方程和直线的极坐标方程；
（2）在（1）的条件下，直线
的极坐标方程为
，设曲线与直线的交于点
和点
，曲线与直线的交于点和点
，求
的面积．
【答案】（1）极坐标方程为：
.直线
的极坐标方程为：
．（2）
【解析】
（1）消去参数φ可得曲线C的直角坐标方程，再根据互化公式可得曲线C的极坐标方程；根据互化公式可得直线l的极坐标方程；（2）根据极径的几何意义和面积公式可得．
（1）由
，
得曲线C的普通方程为
，
把
，
代入该式化简得曲线C的极坐标方程为：.
因为直线：
是过原点且倾斜角为
的直线，
所以直线的极坐标方程为：．
（2）把
代入得
，故
，
把
代入得
，故
，
因为
,
所以
的面积为
.
【题目】C反应蛋白（CRP）是机体受到微生物入侵或组织损伤等炎症性刺激时肝细胞合成的急性相蛋白，医学认为CRP值介于0-10mg/L为正常值下面是某患者在治疗期间连续5天的检验报告单中CRP值（单位：mg/L）与治疗天数的统计数据：
治疗天数x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
（1）若CRP值y与治疗天数x具有线性相关关系，试用最小二乘法求出y关于x的线性回归方程，并估计该患者至少需要治疗多少天CRP值可以到正常水平；
（2）为均衡城乡保障待遇，统一保障范围和支付标准，为参保人员提供公平的基本医疗保障.某市城乡医疗保险实施办法指出：门诊报销比例为50％：住院报销比例，A类医疗机构80％，B类医疗机构60％.若张华参加了城乡基本医疗保险，他因CRP偏高选择在某医疗机构治疗，医生为张华提供了三种治疗方案：
方案一：门诊治疗，预计每天诊疗费80元；
方案二：住院治疗，A类医疗机构，入院检查需花费600元，预计每天诊疗费100元；
方案三：住院治疗，B类医疗机构，入院检查需花费400元，预计每天诊疗费40元；
若张华需要经过连续治疗n天，
，请你为张华选择最经济实惠的治疗方案．
，
.
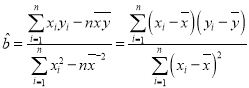【题目】绿水青山就是金山银山．某山村为做好水土保持，退耕还林，在本村的山坡上种植水果，并推出山村游等旅游项目．为预估今年7月份游客购买水果的情况，随机抽样统计了去年7月份100名游客的购买金额．分组如下：
，
，
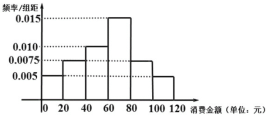
，得到如图所示的频率分布直方图：
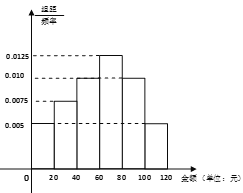
（1）请用抽样的数据估计今年7月份游客人均购买水果的金额（同一组中的数据用该组区间中点作代表）．
（2）若把去年7月份购买水果不低于80元的游客，称为“水果达人”． 填写下面列联表，并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系？
水果达人 | 非水果达人 | 合计 | |
男 | 10 | ||
女 | 30 | ||
合计 |
（3）为吸引顾客，商家特推出两种促销方案．方案一：每满80元可立减10元；方案二：金额超过80元可抽奖三次，每次中奖的概率为
,且每次抽奖互不影响，中奖1次打9折，中奖2次打8折，中奖3次打7折．若每斤水果10元，你打算购买12斤水果，请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案．
附：参考公式和数据：
，
.临界值表：
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
