题目内容
(文)袋中有大小相同的5个白球和3个黑球,从中任意摸出4个,求至少摸出1个黑球的概率
.
| 13 |
| 14 |
| 13 |
| 14 |
分析:先求出试验发生所包含的事件总数,然后求出至少摸出1个黑球的对立事件“4个都是白球”的事件个数,最后根据概率公式解之即可求出所求.
解答:解:由题意知本题是一个等可能事件的概率,
试验发生所包含的事件从袋中装有大小相同的5个白球和3个黑球的袋中摸出4个球,共有C84=70种结果,
满足条件的事件是取出的球中至少摸出1个黑球的情况有三种情况,可考虑对立事件“4个都是白球”共有C54=5
故取出的两个球中至少有一个黑球的概率P=1-
=
故答案为:
试验发生所包含的事件从袋中装有大小相同的5个白球和3个黑球的袋中摸出4个球,共有C84=70种结果,
满足条件的事件是取出的球中至少摸出1个黑球的情况有三种情况,可考虑对立事件“4个都是白球”共有C54=5
故取出的两个球中至少有一个黑球的概率P=1-
| 5 |
| 70 |
| 13 |
| 14 |
故答案为:
| 13 |
| 14 |
点评:本题考查等可能事件的概率,解题的关键是计算出所有取法的基本事件总数,以及利用对立事件的概率公式进行求解,属于中档题.

练习册系列答案
相关题目
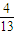 .
.