题目内容
(文)袋中有大小相同的红球和白球若干个,其中红、白球个数的比为4:3.假设从袋中任取2个球,取到的都是红球的概率为
.
(1)试问:袋中的红、白球各有多少个?
(2)从袋中任取3个球,若取到一个红球,则记2分,若取到一个白球,则记1分.试求:所取出球的总分不超过5分的概率.
| 4 |
| 13 |
(1)试问:袋中的红、白球各有多少个?
(2)从袋中任取3个球,若取到一个红球,则记2分,若取到一个白球,则记1分.试求:所取出球的总分不超过5分的概率.
(1)设袋中有红球4k个,白球3k个,由题设
=
,解得k=2,…(4分)
因此,袋中有红球8个,白球6个. …(6分)
(2)从袋中14个球中取出3个球,其可能出现的取法有C143种,即所有的基本事件有C143个. …(8分)
若把“取出球的总分不超过(5分)”的事件记作E,则E所包含的基本事件有C63+C62C81+C61C82个,…(12分)
因此,E出现的概率P(E)=
=
. …(14分)
| ||
|
| 4 |
| 13 |
因此,袋中有红球8个,白球6个. …(6分)
(2)从袋中14个球中取出3个球,其可能出现的取法有C143种,即所有的基本事件有C143个. …(8分)
若把“取出球的总分不超过(5分)”的事件记作E,则E所包含的基本事件有C63+C62C81+C61C82个,…(12分)
因此,E出现的概率P(E)=
| ||||||||||
|
| 11 |
| 13 |

练习册系列答案
相关题目
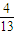 .
.