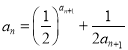题目内容
【题目】已知
为等差数列，
，
，
分别是下表第一、二、三行中的某一个数，且，，中的任何两个数都不在下表的同一列．
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
请从①
，②
，③ 
的三个条件中选一个填入上表，使满足以上条件的数列存在；并在此存在的数列中，试解答下列两个问题
（1）求数列的通项公式；
（2）设数列
满足
，求数列的前n项和
．
【答案】（1）
；（2）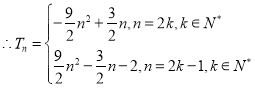
．
【解析】
(1)分别代入①
，②
，③ 
，结合已知条件可判断，
，
，求出数列的公差，即可求出通项公式.
(2)由(1)知
，当n为偶数时，结合数列的求和的定义求出
，
由等差数列的求和公式即可求解；当n为奇数时，
即可求解.
解：（1）若选择条件①，当第一行第一列为
时，由题意知，可能的组合有，
不是等差数列，
不是等差数列；
当第一行第二列为时，由题意知，可能的组合有，
不是等差数列，
不是等差数列；当第一行第三列为时，由题意知，可能的组合有，
不是等差数列，
不是等差数列，
则放在第一行的任何一列，满足条件的等差数列
都不存在，
若选择条件②，则放在第一行第二列，结合条件可知，，，
则公差
，所以
，
，
若选择条件③，当第一行第一列为时，由题意知，可能的组合有，
不是等差数列，
不是等差数列；
当第一行第二列为时，由题意知，可能的组合有，
不是等差数列，
不是等差数列；当第一行第三列为时，由题意知，可能的组合有，
不是等差数列，
不是等差数列，
则放在第一行的任何一列，满足条件的等差数列都不存在，
综上可知：，.
（2）由（1）知，，所以当n为偶数时，
，
当n为奇数时，
，
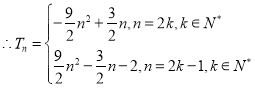
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
