题目内容
1．计算下列不定积分（1）∫$\frac{{3}^{x}-{e}^{x}}{{2}^{x}}$dx；
（2）∫$\frac{1}{{x}^{2}（1+{x}^{2}）}$dx．
分析 根据不定积分的线性运算法则，根据基本不定积分积分的公式，计算即可．
解答 解：（1）∫$\frac{{3}^{x}-{e}^{x}}{{2}^{x}}$dx=${∫}_{\;}^{\;}$$（\frac{3}{2}）^{x}$dx-${∫}_{\;}^{\;}$$（\frac{e}{2}）^{x}$dx=（$\frac{3}{2}$）x•$\frac{1}{ln\frac{3}{2}}$+（$\frac{e}{2}$）x•ln$\frac{e}{2}$+c═（$\frac{3}{2}$）x•$\frac{1}{ln\frac{3}{2}}$+（1-ln2）（$\frac{e}{2}$）x+c，
（2）∫$\frac{1}{{x}^{2}（1+{x}^{2}）}$dx=${∫}_{\;}^{\;}$（$\frac{1}{{x}^{2}}$-$\frac{1}{{x}^{2}+1}$）dx=-$\frac{1}{x}$-arctanx+c．
点评 本题主要考查求不定积分的方法，要求与一定的计算量，以及一些固定函数不定积分的记忆，属于基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
11．将$\root{3}{2^2}$化成分数指数幂为（ ）
| A． | ${2^{\frac{3}{2}}}$ | B． | $2^{-\frac{1}{2}}$ | C． | $2^{\frac{1}{3}}$ | D． | $2^{\frac{2}{3}}$ |
16．下列命题中，正确的是（ ）
| A． | φ=$\frac{π}{4}$是f（x）=3in（x-2φ）的图象关于y轴对称的充分不必要条件 | |
| B． | |$\overrightarrow{a}$|-|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|的充要条件是$\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | |
| C． | a，b，c都为实数，b=$\sqrt{ac}$是a，b，c三数成等比数列的充分不必要条件 | |
| D． | m=3是直线（m+3）x+my-2=0与mx-6y+5=0互相垂直的充要条件 |
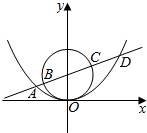如图所示，过抛物线x2=4py（p＞0）焦点的直线依次交抛物线与圆x2+（y-p）2=p2于点A，B，C，D，则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是（ ）