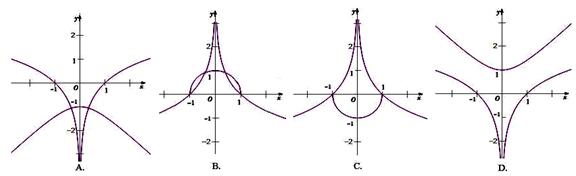
题目内容
已知函数f(x)=|
-1|,其中x∈(o,+∞).
(I)在给定的坐标系中,画出函数f(x)的图象;
(II)设0<a<b,且f(a)=f(b),证明:ab>1.

| 1 |
| x |
(I)在给定的坐标系中,画出函数f(x)的图象;
(II)设0<a<b,且f(a)=f(b),证明:ab>1.

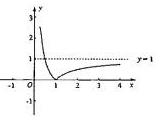
证明:(I)不等式可以变为f(x)=
对函数进行分析知f(x)在(0,1]上是减函数,在(1,+∞)上是增函数.
其图象为:
(II):由题意f(a)=f(b)?|1-
|=|1-
|?(1-
)2=(1-
)2?2ab=a+b≥2
故ab-
≥0,即
(
-1)≥0,
故
-1≥0,故ab>1.
|
对函数进行分析知f(x)在(0,1]上是减函数,在(1,+∞)上是增函数.
其图象为:
(II):由题意f(a)=f(b)?|1-
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| ab |
故ab-
| ab |
| ab |
| ab |
故
| ab |


练习册系列答案
相关题目











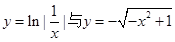 在同一平面直角坐标系内的大致图象为( )
在同一平面直角坐标系内的大致图象为( )