题目内容
18.已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于直线x=1对称,当x∈[-1,0]时,f(x)=-x,则f(2015)+f(2016)=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由函数的对称性可得f(x)=f(2-x),再由奇偶性可得f(x)=-f(x-2),由此可推得函数的周期,根据周期性可把f(2016),f(2015)转化为已知区间上求解
解答 解:因为f(x)图象关于x=1对称,所以f(x)=f(2-x),
又f(x)为奇函数,所以f(2-x)=-f(x-2),即f(x)=-f(x-2),
则f(x+4)=-f(x+2)=-[-f(x)]=f(x),
故4为函数f(x)的一个周期,
从而f(2015)+f(2016)=f(-1)+f(0),
而f(0)=0,f(-1),
故f(-1)+f(0)=1,
即f(2015)+f(2016)=1,
故选:C
点评 本题考查的知识点是函数奇偶性的性质,熟练掌握函数奇偶性的性质,是解答的关键.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
6.如果执行如图的程序框图,那么输出的值是( )
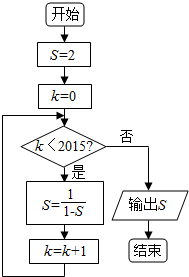

| A. | 2015 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
13. 如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )
如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )
 如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )
如图,四边形ABCD为菱形,四边形CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠BCD=60°,若二面角D-CE-F的大小为α,异面直线BC与AE所成角的大小为β,则( )| A. | tanα=$\sqrt{3}$,tanβ=$\frac{\sqrt{7}}{3}$ | B. | tanα=$\frac{\sqrt{7}}{3}$,tanβ=$\sqrt{3}$ | ||
| C. | tanα=$\frac{2\sqrt{3}}{3}$,tanβ=$\frac{\sqrt{6}}{3}$ | D. | tanα=$\frac{\sqrt{7}}{3}$,tanβ=$\frac{\sqrt{6}}{3}$ |
3.下列命题中为真命题的是( )
| A. | 命题“若x>1,则x2>1”的否命题 | |
| B. | 命题“若x>y,则|x|>y”的逆命题 | |
| C. | 若k<5,则两椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$与$\frac{x^2}{9-k}+\frac{y^2}{5-k}=1$有不同的焦点 | |
| D. | 命题“若方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围为(0,1)”的逆否命题 |
7.下列函数中,既是偶函数又在区间(0,+∞)上是增函数的是( )
| A. | y=-x2 | B. | y=ex-e-x | C. | y=ln(|x|+1) | D. | y=x•sinx+cosx |



