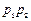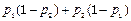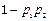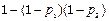题目内容
甲、乙两人破译一密码,它们能破译的概率分别为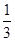 和
和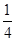 ,试求:
,试求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少乙这样的人?
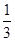 和
和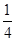 ,试求:
,试求:(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少乙这样的人?
(1)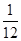 (2)
(2)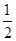 (3)
(3) (4)
(4) (5)16个
(5)16个
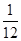 (2)
(2)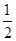 (3)
(3) (4)
(4) (5)16个
(5)16个解:设事件A为“甲能译出”,事件B为“乙能译出”,则A、B相互独立,从而A与
 、
、 与B、
与B、 与
与 均相互独立.
均相互独立.(1)“两人都能译出”为事件AB,则
P(AB)=P(A)P(B)=
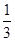 ×
×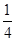 =
=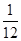 .
.(2)“两人都不能译出”为事件

 ,则
,则P(

 )=P(
)=P( )P(
)P( )=[1-P(A)][1-P(B)]
)=[1-P(A)][1-P(B)]=
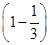
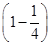 =
=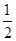 .
.(3)“恰有一人能译出”为事件A
 +
+ B,又A
B,又A 与
与 B互斥,则P(A
B互斥,则P(A +
+ B)=P(A
B)=P(A )+P(
)+P( B)
B)=P(A)P(
 )+P(
)+P( )P(B)
)P(B)=
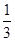 ×
×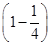 +
+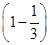 ×
×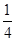 =
= .
.(4)“至多一人能译出”为事件A
 +
+ B+
B+
 ,且A
,且A 、
、 B、
B、
 互斥,故
互斥,故P(A
 +
+ B+
B+
 )
)=P(A)P(
 )+P(
)+P( )P(B)+P(
)P(B)+P( )P(
)P( )
)=
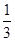 ×
×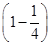 +
+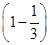 ×
×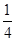 +
+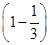 ×
×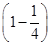 =
= .
.(5)设至少需n个乙这样的人,而n个乙这样的人译不出的概率为
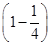 n,故n个乙这样的人能译出的概率为1-
n,故n个乙这样的人能译出的概率为1-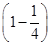 n≈99%.
n≈99%.解得n=16.
故至少需16个乙这样的人,才能使译出的概率为99%.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
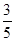 ,且每次射击的结果互不影响,已知射手射击了5
,且每次射击的结果互不影响,已知射手射击了5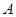 发生的概率为
发生的概率为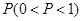 ,则事件
,则事件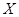 的方差的最大值为( )
的方差的最大值为( )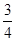
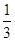
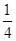

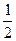 ,构造数列
,构造数列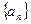 ,使
,使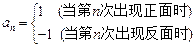 ,记
,记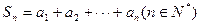 .
.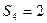 的概率;
的概率;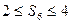 的概率.
的概率.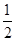 ,乙能解决的概率为
,乙能解决的概率为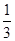 ,两人试图独立地在半小时解决,则两人都未解决的概率为________.
,两人试图独立地在半小时解决,则两人都未解决的概率为________.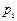 ,乙解决这个问题的概率是
,乙解决这个问题的概率是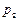 ,那么恰好有1人解决这个问题的概率是 ( )
,那么恰好有1人解决这个问题的概率是 ( )