题目内容
设函数f(x)的定义域为R,且f(x)是以3为周期的奇函数,f(1)>1,f(2)=loga2(a>0,且a≠1),则实数a的取值范围是
- A.a>1
- B.0<a<1或a>2
- C.

- D.0<a<1
C
分析:先根据函数的周期性得到f(2)=f(-1),再借助于f(x)为R上的奇函数求出f(1)的值,最后通过对对数函数底数的讨论分情况求出a的取值范围.
解答:∵f(x)是以3为周期的函数,
∴f(2)=f(-1)=loga2;
∵f(x)为R上的奇函数
∴f(-1)=-f(1),
∴f(1)=-loga2.
∴f(1)>1?-loga2>1?loga2<-log aa.
所以有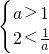 或
或 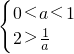 ,
,
所以 <a<1.
<a<1.
故选C.
点评:本题主要考查函数奇偶性与周期性的综合应用,以及对数不等式的解法.在解对数不等式时,一定要分底数大于1和底数大于0小于1两种情况来解.
分析:先根据函数的周期性得到f(2)=f(-1),再借助于f(x)为R上的奇函数求出f(1)的值,最后通过对对数函数底数的讨论分情况求出a的取值范围.
解答:∵f(x)是以3为周期的函数,
∴f(2)=f(-1)=loga2;
∵f(x)为R上的奇函数
∴f(-1)=-f(1),
∴f(1)=-loga2.
∴f(1)>1?-loga2>1?loga2<-log aa.
所以有
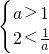 或
或 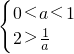 ,
,所以
 <a<1.
<a<1.故选C.
点评:本题主要考查函数奇偶性与周期性的综合应用,以及对数不等式的解法.在解对数不等式时,一定要分底数大于1和底数大于0小于1两种情况来解.

练习册系列答案
相关题目
 )与b=f(
)与b=f( )的大小关系为________.
)的大小关系为________. )与b=f(
)与b=f( )的大小关系为 .
)的大小关系为 . )与b=f(
)与b=f( )的大小关系为( ).
)的大小关系为( ).