题目内容

13．在菱形ABCD中，|$\overrightarrow{AB}$|=2，∠BAD=$\frac{π}{3}$，E为CD的中点，则$\overrightarrow{AC}$•$\overrightarrow{BE}$=（　　）
A．-3B．3C．$\sqrt{3}$D．0

分析 建立坐标系得出A，B，C，D，E的坐标，运用向量的坐标运算即可．

解答 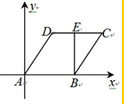解；建立坐标系如图，则A（0，0），B（2，0），C（3，$\sqrt{3}$），D（1，$\sqrt{3}$），E（2，$\sqrt{3}$），$\overrightarrow{BE}$=（0，$\sqrt{3}$）
$\overrightarrow{AC}$$•\overrightarrow{BE}$=3
故选：B

点评 本题考察了菱形的几何性质，平面向量的坐标运算，属于容易题，关键是确定准点的坐标．

练习册系列答案
相关题目
3．已知函数f（x）=$\frac{\sqrt{2}}{2}$sin2x-cos2x，x∈R．
（1）当x∈[0，π]时，求函数f（x）的单调增区间；
（2）设△ABC的内角A、B、C的对边分别为a、b、c，且c=$\sqrt{3}$，f（C）=0，若向量$\overrightarrow{m}$=（1，sinA）与向量$\overrightarrow{n}$=（2，sinB）共线，求△ABC的面积．
4．在等比数列{an}中，a1=2，q=2，则其通项公式为（　　）
A．an=2n-1B．an=2nC．an=2n+1D．an=2n+1
1．抛掷一枚均匀硬币n（3≤n≤8）次，正面向上的次数ξ服从二项分布B（n，$\frac{1}{2}$），若P（ξ=1）=$\frac{3}{32}$，则方差D（ξ）=$\frac{3}{2}$．
8．已知cosα=-$\frac{3}{5}$，且α∈（-π，0），则tanα=（　　）
A．-$\frac{4}{3}$B．$\frac{4}{3}$C．-$\frac{3}{4}$D．$\frac{3}{4}$
18．顺次列出的规律相同的20个数中的前四个数依次是2×1-1，2×2-1，2×3-1，2×4-1，第15个数是（　　）
A．15B．29C．16D．31
5．f′（x）是定义在R上的函数f（x）的导函数，x0∈R，设命题P：f′（x0）=0；命题Q：x=x0是函数f（x）的极值点，则P是Q成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
2．已知函数f（x）=$\frac{lnx}{x}$（0＜x＜1），则下列不等式正确的是（　　）
A．f2（x）＜f（x2）＜f（x）B．f（x2）＜f2（x）＜f（x）C．f（x）＜f（x2）＜f2（x）D．f（x2）＜f（x）＜f2（x）
3．化简$\sqrt{1+sin4}+\sqrt{1-sin4}$，得到（　　）
A．-2sin2B．-2cos2C．2sin2D．2cos2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网