题目内容
【题目】某中学在全校范围内举办了一场“中国诗词大会”的比赛,规定初赛测试成绩不小于160分的学生进入决赛阶段比赛.现有200名学生参加测试,并将所有测试成绩统计如下表:
分数段 | 频数 | 频率 |
| 6 | 0.03 |
|
| 0.38 |
| 100 | 0.5 |
|
|
|
| 6 | 0.03 |
合计 | 200 | 1 |
(1)计算![]() 的值;
的值;
(2)现利用分层抽样的方法从进入决赛的学生中选择6人,再从选出的6人中选2人做进一步的研究,求选择的2人中至少有1人的分数在![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由频率和为1,求出![]() ,从而求出
,从而求出![]() ,再由频数和为200,求出
,再由频数和为200,求出![]() ;
;
(2)按比例求出两组抽取的人数,并把6人编号,所求事件的概率为古典概型的概率,列出6人中选2人的所有情况,找出至少有1人的分数在![]() 的选法, 即可求出概率
的选法, 即可求出概率
(1)![]() ,
,
![]() ,
,
![]() ;
;
(2)利用分层抽样的方法从进入决赛的学生中选择6人,
则![]() 组中选4人,记为1,2,3,4;
组中选4人,记为1,2,3,4;
![]() 组选2人,记为A,B. 从选出的6人中选2人
组选2人,记为A,B. 从选出的6人中选2人
所有情况有:{1,2},{1,3},{1,4},{1,A},{1,B},{2,3},{2,4},
{2,A},{2,B},{3,4},{3,A},{3,B},{4,A},{4,B},{A,B}.共有15
种选法,选择的2人中至少有1人的分数在![]() 有9种选法.
有9种选法.
![]() 选择的2人中至少有1人的分数在
选择的2人中至少有1人的分数在![]() 的概率为
的概率为![]() .
.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成![]() ,
,![]() 两组,每组20人,
两组,每组20人,![]() 组群众给第一阶段的创文工作评分,
组群众给第一阶段的创文工作评分,![]() 组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
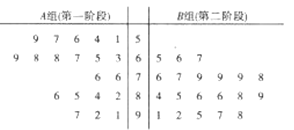
(Ⅰ)根据茎叶图比较群众对两个阶段的创文工作满意度评分的平均值和集中程度(不要求计算出具体值,给出结论即可);
(Ⅱ)完成下面的列联表,并通过计算判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | 合计 | |
第一阶段 | |||
第二阶段 | |||
合计 |
参考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |


