题目内容
已知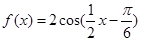 ,
,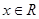 。
。
(1)求 的振幅,最小正周期,对称轴,对称中心。
的振幅,最小正周期,对称轴,对称中心。
(2)说明 是由余弦曲线经过怎样变换得到。
是由余弦曲线经过怎样变换得到。
(1)振幅为2,最小正周期为 ,对称轴为
,对称轴为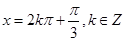 ,对称中心为
,对称中心为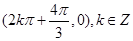 ;(2)利用三角变换即可得到
;(2)利用三角变换即可得到
解析试题分析:(1)因为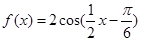 ,所以振幅为2,最小正周期为
,所以振幅为2,最小正周期为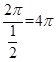 ,令
,令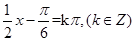 得函数的对称轴为
得函数的对称轴为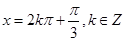 ,令
,令 得函数的对称中心为
得函数的对称中心为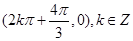
(2)将y=cosx先向右平移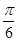 个单位,然后横坐标扩大到原来的2倍(纵坐标不变),再把纵坐标扩大到了原来的2倍(横坐标不变)即可得到曲线
个单位,然后横坐标扩大到原来的2倍(纵坐标不变),再把纵坐标扩大到了原来的2倍(横坐标不变)即可得到曲线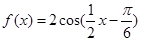
考点:本题考查了三角函数的变换及性质
点评:解答三角函数的图象变换问题,关键是要分析清楚平移或伸缩的单位和倍数,要准确理解变换的法则

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目

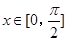 ,
, 的最小值是
的最小值是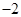 ,最大值是
,最大值是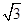 ,求实数
,求实数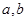 的值.
的值.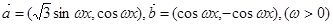 ,函数
,函数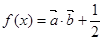 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为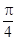 .
.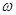 的值;
的值;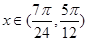 ,
,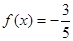 ,求
,求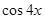 的值;
的值;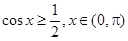 ,且
,且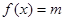 有且仅有一个实根,求实数
有且仅有一个实根,求实数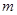 的值.
的值. ,其图象过点
,其图象过点
 的值;
的值;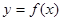 图象上各点向左平移
图象上各点向左平移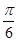 个单位长度,得到函数
个单位长度,得到函数 的图象,求函数
的图象,求函数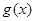 在
在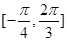 上的单调递增区间.
上的单调递增区间.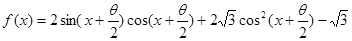
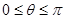 ,求
,求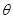 使函数
使函数 为偶函数。
为偶函数。 ∈[-π,π]的
∈[-π,π]的 ,
,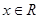 的最大值是1且其最小正周期为
的最大值是1且其最小正周期为 .
.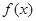 的解析式;
的解析式; ,且
,且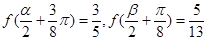 ,求
,求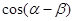 的值.
的值.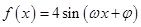 ,
,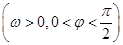 ,
,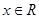 的最小正周期是
的最小正周期是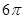 ,其图象经过点
,其图象经过点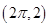 .
.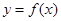 的表达式;
的表达式;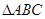 的三个内角分别为
的三个内角分别为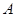 ,
,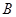 ,
,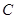 ,若
,若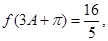
 ;求
;求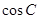 的值.
的值. ,且函数
,且函数 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为 .
.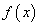 的对称中心;
的对称中心;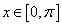 时,求
时,求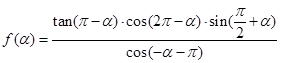 .
.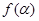 ;
;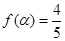 ,且
,且 是第二象限角,求
是第二象限角,求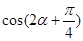 的值.
的值.