题目内容
已知函数 ,且函数
,且函数 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为 .
.
(Ⅰ)求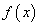 的对称中心;
的对称中心;
(Ⅱ)当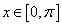 时,求
时,求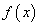 的单调增区间.
的单调增区间.
(Ⅰ)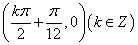 (Ⅱ)
(Ⅱ)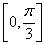 ,
,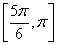
解析试题分析:(Ⅰ) .
.
由题意,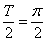 ,即
,即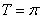 ,所以
,所以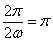 ,即
,即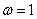 .
.
从而 , 4分
, 4分
令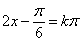 ,则
,则 所以对称中心为
所以对称中心为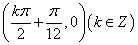 6分
6分
(Ⅱ) 由
由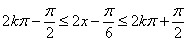
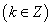 可得:
可得: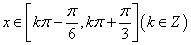 时
时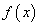 为单调递增函数 8分
为单调递增函数 8分
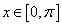 ∴
∴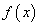 单调递增区间为
单调递增区间为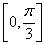 ,
,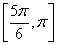 12分
12分
考点:三角函数化简及性质
点评:要考察三角函数性质先要将其整理为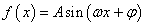 的形式,其周期性由
的形式,其周期性由 决定,对称中心是函数与x轴交点的坐标,求单调增区间时首先令
决定,对称中心是函数与x轴交点的坐标,求单调增区间时首先令 进而解不等式求x的范围
进而解不等式求x的范围

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
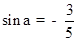 ,且
,且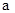 为第三象限角,求
为第三象限角,求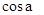 ,
,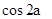 的值
的值
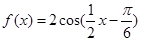 ,
,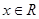 。
。 的振幅,最小正周期,对称轴,对称中心。
的振幅,最小正周期,对称轴,对称中心。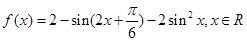 ,记
,记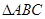 的内角
的内角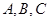 的对边长分别为
的对边长分别为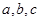 ,若
,若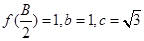 ,求
,求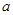 的值。
的值。 是△
是△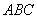 的三个内角,向量
的三个内角,向量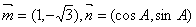 ,且
,且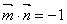
 ;
;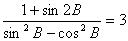 ,求
,求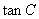 的值。
的值。 .
.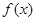 的最小正周期和单调增区间;
的最小正周期和单调增区间;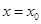 对称,且
对称,且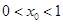 ,求
,求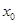 的值.
的值.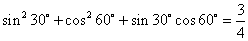 ;
;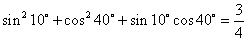 ;
;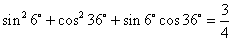 .
.
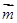 =(
=( sin
sin ,1),
,1),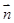 =(cos
=(cos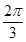 -x)的值;
-x)的值;