题目内容
设F1和F2为双曲线 的两个焦点,点P在双曲线上,且满足∠F1PF2=900,则⊿F1PF2的面积是 ( )
的两个焦点,点P在双曲线上,且满足∠F1PF2=900,则⊿F1PF2的面积是 ( )
| A.1 | B.2 | C.3 | D.4 |
A
解析试题分析:设|PF1|=x,|PF2|=y,(x>y)
根据双曲线性质可知x-y=4,∵∠F1PF2=90°,∴x2+y2=20∴2xy=x2+y2-(x-y)2=4
∴xy=2∴△F1PF2的面积 xy=1
xy=1
故答案为A
考点:本试题主要考查了双曲线的简单性质.要灵活运用双曲线的定义及焦距、实轴、虚轴等之间的关系.
点评:解决该试题的关键是灵活运用双曲线的定义和勾股定理来得到|PF1||PF2|的值,进而结合正弦面积公式得到求解面积的值。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
抛物线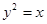 的准线方程是
的准线方程是
A.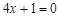 | B.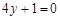 |
C.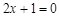 | D.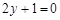 |
已知双曲线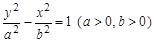 的离心率是
的离心率是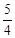 ,其焦点为
,其焦点为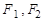 ,P是双曲线上一点,
,P是双曲线上一点,
且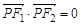 ,若
,若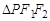 的面积等于9,则
的面积等于9,则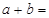 ( )
( )
| A.5 | B.6 | C.7 | D.8 |
双曲线 的焦距是
的焦距是
| A.4 | B.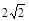 | C.8 | D.与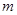 有关 有关 |
直线 与椭圆
与椭圆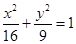 相交于
相交于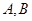 两点,该椭圆上点
两点,该椭圆上点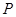 使
使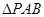 的面积等于6,这样的点
的面积等于6,这样的点 共有( )
共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设椭圆的标准方程为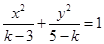 ,若其焦点在
,若其焦点在 轴上,则
轴上,则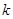 的取值范围是( )
的取值范围是( )
A.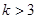 | B.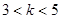 | C.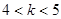 | D.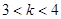 |
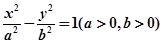 的右焦点
的右焦点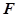 作圆
作圆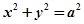 的切线
的切线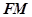 (切点为
(切点为 ),交
),交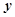 轴于点
轴于点 .若
.若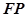 的中点,则双曲线的离心率为( )
的中点,则双曲线的离心率为( )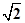
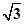
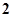
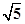
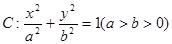 的左顶点A的斜率为
的左顶点A的斜率为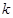 的直线交椭圆C于另一个点B,且点B在
的直线交椭圆C于另一个点B,且点B在 上
上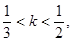 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )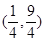

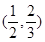
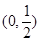
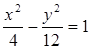 ,则它的一个焦点到一条渐进线的距离是( )
,则它的一个焦点到一条渐进线的距离是( )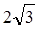 D. 12
D. 12