题目内容
已知椭圆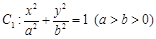 经过点
经过点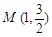 ,且其右焦点与抛物线
,且其右焦点与抛物线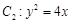 的焦点
的焦点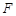 重合,过点
重合,过点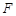 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于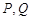 两点.
两点.
(1)求椭圆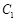 的方程;
的方程;
(2)设O为坐标原点,线段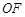 上是否存在点
上是否存在点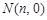 ,使得
,使得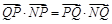 ?
?
若存在,求出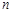 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)过点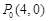 且不垂直于
且不垂直于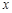 轴的直线与椭圆交于
轴的直线与椭圆交于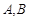 两点,点
两点,点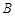 关于
关于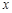 轴的对称点为
轴的对称点为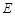 ,
,
试证明:直线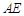 过定点.
过定点.
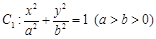 经过点
经过点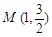 ,且其右焦点与抛物线
,且其右焦点与抛物线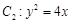 的焦点
的焦点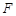 重合,过点
重合,过点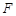 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于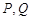 两点.
两点.(1)求椭圆
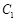 的方程;
的方程;(2)设O为坐标原点,线段
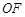 上是否存在点
上是否存在点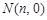 ,使得
,使得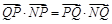 ?
?若存在,求出
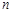 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;(3)过点
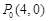 且不垂直于
且不垂直于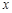 轴的直线与椭圆交于
轴的直线与椭圆交于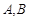 两点,点
两点,点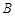 关于
关于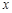 轴的对称点为
轴的对称点为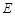 ,
,试证明:直线
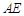 过定点.
过定点.(1)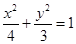
(2)存在,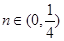
(3)详见解析
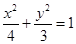
(2)存在,
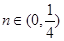
(3)详见解析
解:(1)由题意,得:
所以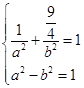 , 解,得
, 解,得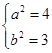 ,所以椭圆的方程为:
,所以椭圆的方程为: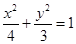 ;
;
(2)设直线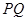 的方程为:
的方程为: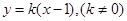 ,代入
,代入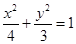 ,得:
,得:

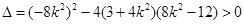 恒成立.
恒成立.
设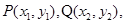 线段
线段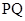 的中点为
的中点为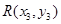 ,
,
则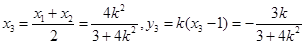 ,
,
由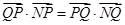 得:
得: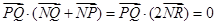 ,
,
所以直线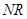 为直线
为直线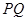 的垂直平分线,
的垂直平分线,
直线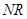 的方程为:
的方程为: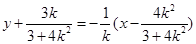 ,
,
令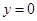 得:
得: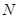 点的横坐标
点的横坐标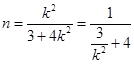 ,
,
因为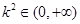 , 所以
, 所以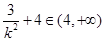 ,所以
,所以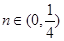 .
.
所以线段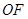 上存在点
上存在点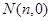 使得
使得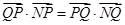 ,其中
,其中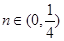 .
.
证明:设直线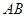 的方程为:
的方程为: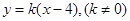 ,代入
,代入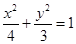 ,得:
,得:
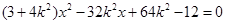 ,
,
由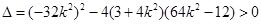 ,得:
,得: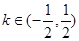 ,
,
设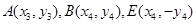 ,则
,则
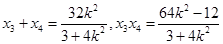 ,
,
则直线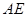 的方程为
的方程为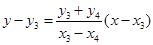 ,
,
令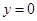 得:
得: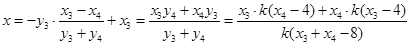
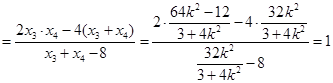 ,
,
所以直线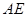 过定点
过定点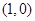 .
.

所以
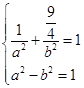 , 解,得
, 解,得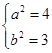 ,所以椭圆的方程为:
,所以椭圆的方程为: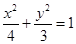 ;
;(2)设直线
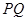 的方程为:
的方程为: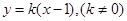 ,代入
,代入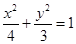 ,得:
,得:
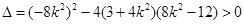 恒成立.
恒成立.设
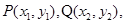 线段
线段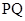 的中点为
的中点为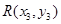 ,
,则
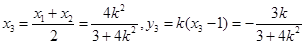 ,
,由
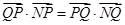 得:
得: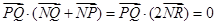 ,
,所以直线
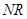 为直线
为直线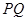 的垂直平分线,
的垂直平分线,直线
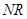 的方程为:
的方程为: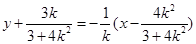 ,
,令
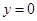 得:
得: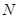 点的横坐标
点的横坐标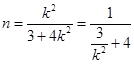 ,
, 因为
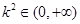 , 所以
, 所以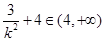 ,所以
,所以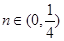 .
.所以线段
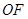 上存在点
上存在点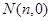 使得
使得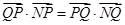 ,其中
,其中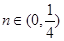 .
.证明:设直线
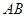 的方程为:
的方程为: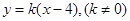 ,代入
,代入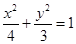 ,得:
,得: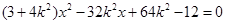 ,
,由
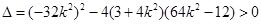 ,得:
,得: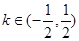 ,
,设
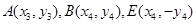 ,则
,则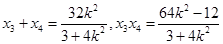 ,
,则直线
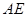 的方程为
的方程为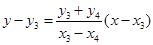 ,
,令
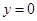 得:
得: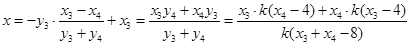
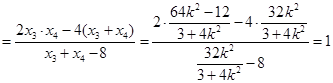 ,
,所以直线
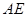 过定点
过定点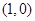 .
.
练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
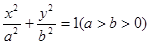 的左右焦点分别为
的左右焦点分别为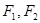 ,短轴两个端点为
,短轴两个端点为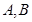 ,且四边形
,且四边形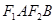 是边长为2的正方形.
是边长为2的正方形.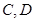 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点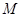 满足
满足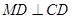 ,连接
,连接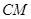 ,交椭圆于点
,交椭圆于点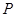 .证明:
.证明: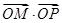 为定值;
为定值;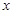 轴上是否存在异于点
轴上是否存在异于点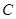 的定点
的定点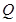 ,使得以
,使得以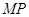 为直径的圆恒过直线
为直径的圆恒过直线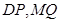 的交点,若存在,求出点
的交点,若存在,求出点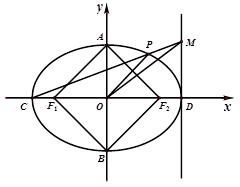
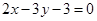 和
和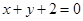 的交点且与直线
的交点且与直线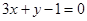 垂直的直线方程.
垂直的直线方程.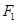 ,
,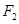 是双曲线
是双曲线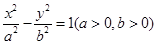 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点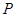 与点
与点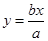 对称,则该双曲线的离心率为 ( )
对称,则该双曲线的离心率为 ( )



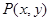 满足到定点
满足到定点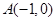 的距离与到定点
的距离与到定点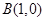 距离之比为
距离之比为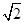 .
.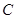 的方程;
的方程;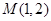 的直线
的直线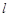 与曲线
与曲线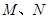 ,若
,若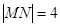 ,求直线
,求直线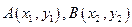 分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB中点M到原点距离的最小值为( ).
分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB中点M到原点距离的最小值为( ).


