题目内容
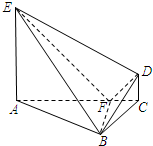 (2012•漳州模拟)如图,在Rt△ABC中,∠ABC=3∠BAC=90°,BF⊥AC垂足是F,AE⊥平面ABC,CD∥AE,AC=4CD=4,AE=3.
(2012•漳州模拟)如图,在Rt△ABC中,∠ABC=3∠BAC=90°,BF⊥AC垂足是F,AE⊥平面ABC,CD∥AE,AC=4CD=4,AE=3.(Ⅰ)求证:BE⊥DF;
(Ⅱ)求二面角B-DE-F的平面角的余弦值.
分析:(Ⅰ)先根据条件得到平面AEC⊥平面ABC;进而得到BF⊥平面AEC,即可得到BF⊥DF;进而根据条件得到DF⊥平面BEF即可证明结论;
(Ⅱ)先建立空间直角坐标系,求出各点的坐标,进而求出两个平面的法向量的坐标,最后代入夹角计算公式即可求出结论.
(Ⅱ)先建立空间直角坐标系,求出各点的坐标,进而求出两个平面的法向量的坐标,最后代入夹角计算公式即可求出结论.
解答:解: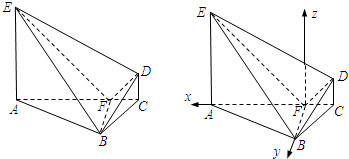 (Ⅰ)证明:∵AE⊥平面ABC,AE?平面AEC,
(Ⅰ)证明:∵AE⊥平面ABC,AE?平面AEC,
∴平面AEC⊥平面ABC,平面AEC∩平面ABC=AC,
BF?平面ABC,BF⊥AC,∴BF⊥平面AEC,DF?平面AEC,
∴BF⊥DF,
又∠ABC=3∠BAC=90°,∴BC=ACsin30°=4×
=2,BF⊥AC,
∴CF=BCcos60°=1=CD,CD∥AE,AE⊥平面ABC,
∴CD⊥平面ABC,∴CD⊥AC,∴∠DFC=45°,
AF=AC-CF=3=AE,∴∠EFA=45°,
∴∠EFD=90°,即DF⊥EF,
BF∩EF=F,BF、EF?平面BEF,∴DF⊥平面BEF,
∴DF⊥BE.
(Ⅱ)过F作Fz∥AE,由AE⊥平面ABC可知Fz⊥平面ABC,
又BF⊥AC,∴BF、AC、l两两垂直,
以F为原点,FA、FB、Fz依次为x、y、z轴建立空间直角坐标系(如图),
则F(0,0,0),B(0 ,
, 0),D(-1,0,1),E(3,0,3),
=(-1 , -
, 1),
=(3 , -
, 3),
=(0 ,
, 0),
由(Ⅰ)知
是平面DEF的一个法向量,设
=(x ,y ,z)是平面BDE的一个法向量,
则
取z=2,得到
=(-1 ,
, 2),
cos<
,
>=
=
=
,
∴二面角B-DE-F的平面角的余弦值为
.
 (Ⅰ)证明:∵AE⊥平面ABC,AE?平面AEC,
(Ⅰ)证明:∵AE⊥平面ABC,AE?平面AEC,∴平面AEC⊥平面ABC,平面AEC∩平面ABC=AC,
BF?平面ABC,BF⊥AC,∴BF⊥平面AEC,DF?平面AEC,
∴BF⊥DF,
又∠ABC=3∠BAC=90°,∴BC=ACsin30°=4×
| 1 |
| 2 |
∴CF=BCcos60°=1=CD,CD∥AE,AE⊥平面ABC,
∴CD⊥平面ABC,∴CD⊥AC,∴∠DFC=45°,
AF=AC-CF=3=AE,∴∠EFA=45°,
∴∠EFD=90°,即DF⊥EF,
BF∩EF=F,BF、EF?平面BEF,∴DF⊥平面BEF,
∴DF⊥BE.
(Ⅱ)过F作Fz∥AE,由AE⊥平面ABC可知Fz⊥平面ABC,
又BF⊥AC,∴BF、AC、l两两垂直,
以F为原点,FA、FB、Fz依次为x、y、z轴建立空间直角坐标系(如图),
则F(0,0,0),B(0 ,
| 3 |
| BD |
| 3 |
| BE |
| 3 |
| FB |
| 3 |
由(Ⅰ)知
| FB |
| n |
则
|
| n |
| 3 |
cos<
| n |
| FB |
| ||||
|
|
| 3 | ||||
2
|
| ||
| 4 |
∴二面角B-DE-F的平面角的余弦值为
| ||
| 4 |
点评:本题主要考察线线垂直的证明以及二面角的求法.一般在证明线线垂直时,是转化为线面垂直来证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
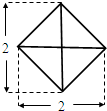 (2012•漳州模拟)一个几何体的正视图、侧视图、俯视图都是如图所示正方形及其对角线,则该几何体的体积等于( )
(2012•漳州模拟)一个几何体的正视图、侧视图、俯视图都是如图所示正方形及其对角线,则该几何体的体积等于( ) (2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )
(2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )