题目内容
设函数 的图像与y轴交点为
的图像与y轴交点为 ,且曲线在
,且曲线在 点处的切线方程为
点处的切线方程为 ,若函数在
,若函数在 处取得极值为
处取得极值为 .(1)求函数解析式;(2)确定函数的单调递增区间;(3)证明:当
.(1)求函数解析式;(2)确定函数的单调递增区间;(3)证明:当 (14分)
(14分)
【答案】
解(1)因为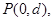 …………………………………………………(1分)
…………………………………………………(1分)
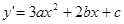 ,由题意得如下方程组
,由题意得如下方程组
 .………………………………………(5分)
.………………………………………(5分)
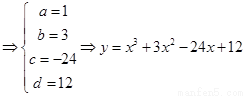 …………………………(7分)
…………………………(7分)
(2) 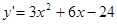 ,令
,令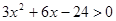 ,解得
,解得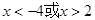 , (8分)
, (8分)
所以函数的单调递增区间是 . ………………………(9分)
. ………………………(9分)
(3)令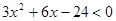 ,解得
,解得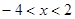 ,
,
所以,原函数的减区间是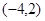 , …………………………………………(10分)
, …………………………………………(10分)
再由(2)可知,当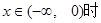 ,
,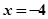 是原函数的极大值点,且是唯一的极值点(11分)
是原函数的极大值点,且是唯一的极值点(11分)
所以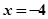 时的函数值是最大值, …………………………………………(12分)
时的函数值是最大值, …………………………………………(12分)
所以当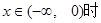 ,
,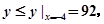 …………………………………(13分)
…………………………………(13分)
所以,
当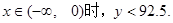 恒成立. ……………………………(14分)
恒成立. ……………………………(14分)
【答案】
【解析】略

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
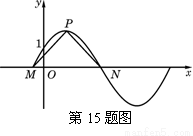
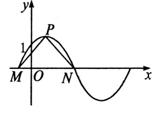
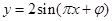 ,x∈R,(其中0≤
,x∈R,(其中0≤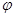 ≤
≤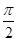 )的图像与y轴交于点(0,1). 设P是图像上的最高点,M、N是图像与x轴的交点,则
)的图像与y轴交于点(0,1). 设P是图像上的最高点,M、N是图像与x轴的交点,则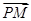 与
与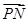 的夹角的余弦值为
的夹角的余弦值为