题目内容
已知函数f(x)在其定义域上满足:xf(x)+2af(x)=x+a-1,a>0.
①函数y=f(x)的图象是否是中学对称图形?若是,请指出其对称中心(不证明);
②当f(x)∈[
,
]时,求x的取值范围;
③若f(0)=0,数列{an}满足a1=1,那么若0<an+1≤f(an)正整数N满足n>N时,对所有适合上述条件的数列{an},an<
恒成立,求最小的N.
①函数y=f(x)的图象是否是中学对称图形?若是,请指出其对称中心(不证明);
②当f(x)∈[
| 1 |
| 2 |
| 4 |
| 5 |
③若f(0)=0,数列{an}满足a1=1,那么若0<an+1≤f(an)正整数N满足n>N时,对所有适合上述条件的数列{an},an<
| 1 |
| 10 |
分析:①化简函数y=f(x)的表达式,通过反比例函数判断函数的图象是对称图形,直接指出其对称中心;
②通过f(x)∈[
,
],转化分式不等式与不等式组的形式,然后求x的取值范围;
③利用f(0)=0,推出a=1,求出函数的表达式,通过0<an+1≤f(an)构造bn=
+1,推出an≤
,结合an<
恒成立,可求n的最小值,即可求最小的N.
②通过f(x)∈[
| 1 |
| 2 |
| 4 |
| 5 |
③利用f(0)=0,推出a=1,求出函数的表达式,通过0<an+1≤f(an)构造bn=
| 1 |
| an |
| 1 |
| 2n-1 |
| 1 |
| 10 |
解答:解:①∵xf(x)+2af(x)=x+a-1
∴(x+2a)f(x)=x+a-1.若x=-2a时,则a=-1,与a>0矛盾
∴x≠-2a,∴f(x)=
=1-
(x≠-2a)
∴f(x)是中心对称图形,对称中心为(-2a,1)
②∵f(x)∈[
,
],
≤
≤
⇒
⇒
又a>0,所以
⇒2≤x≤3a+5
③∵f(0)=0,∴a=1,∴f(x)=
由0<an+1≤f(an)⇒
≥2×
+1,即
+1≥2(
+1),令bn=
+1
∴bn+1≤bn,又an>0,∴
≥2,又a1=1,∴b1=2
当n≥2,bn=b1×
×
×…×
≥2×2×2×…×2=2n
(或bn≥2bn-1≥22bn-2≥23bn-3≥…≥2n-1b1=2n)
又∵b1=1也符合,bn≥2n,∴bn≥2n(n∈N*)
即
+1≥2n⇒an≤
,(n∈N*)
要使an<
恒成立,只需
<
即2n>11.
∴n>3.
所以N=3
∴(x+2a)f(x)=x+a-1.若x=-2a时,则a=-1,与a>0矛盾
∴x≠-2a,∴f(x)=
| x+a-1 |
| x+2a |
| a+1 |
| x+2a |
∴f(x)是中心对称图形,对称中心为(-2a,1)
②∵f(x)∈[
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| x+a-1 |
| x+2a |
| 4 |
| 5 |
|
|
又a>0,所以
|
③∵f(0)=0,∴a=1,∴f(x)=
| x |
| x+2 |
由0<an+1≤f(an)⇒
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
∴bn+1≤bn,又an>0,∴
| bn+1 |
| bb |
当n≥2,bn=b1×
| b2 |
| b1 |
| b3 |
| b2 |
| bn |
| bn-1 |
(或bn≥2bn-1≥22bn-2≥23bn-3≥…≥2n-1b1=2n)
又∵b1=1也符合,bn≥2n,∴bn≥2n(n∈N*)
即
| 1 |
| an |
| 1 |
| 2n-1 |
要使an<
| 1 |
| 10 |
| 1 |
| 2n-1 |
| 1 |
| 10 |
∴n>3.
所以N=3
点评:本题考查函数的性质的应用,函数的值域的应用,不等式组的解法,数列与函数的综合应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
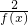 在M内为增函数.
在M内为增函数.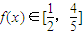 时,求x的取值范围;
时,求x的取值范围; 恒成立,求最小的N;
恒成立,求最小的N; .
.