��Ŀ����
��֪����f��x�����䶨����������xf��x��+2af��x��=x+a-1��a��0����
��1������y=f��x����ͼ���Ƿ������ĶԳ�ͼ�Σ����ǣ���ָ����Գ����ģ���֤������
��2����f(x)��[
��
]ʱ����x��ȡֵ��Χ��
��3����f��0��=0������{an}����a1=1����ô��
����0��an+1��f��an����������N����n��Nʱ���������ʺ���������������{an}��an��
�������������N��
����an+1=f��an������֤��a1a2+a2a3+a3a4+��+anan+1��
��
��1������y=f��x����ͼ���Ƿ������ĶԳ�ͼ�Σ����ǣ���ָ����Գ����ģ���֤������
��2����f(x)��[
| 1 |
| 2 |
| 4 |
| 5 |
��3����f��0��=0������{an}����a1=1����ô��
����0��an+1��f��an����������N����n��Nʱ���������ʺ���������������{an}��an��
| 1 |
| 10 |
����an+1=f��an������֤��a1a2+a2a3+a3a4+��+anan+1��
| 3 |
| 7 |
��������1���������У�x+2a��f��x��=x+a-1����x=-2a����a=-1������a��0ì�ܣ���x��-2a������f(x)=
=1-
(x��-2a)���ɴ�֪y=f��x����ͼ�������ĶԳ�ͼ�Σ����������Գ����ģ�
��2����f(x)��[
��
]��֪
����a��0�������x��ȡֵ��Χ��
��3������f��0��=0��a=1����f(x)=
����0��an+1��
����
+1��2(
+1)����bn=
+1����bn+1��2bn���ɴ������Ƶ�����������Ҫ�����С��������
����an=
��֪anan+1=
��a1a2=
��
��a1a2+a2a3=
+
=
��
���ʵ�n=1��2ʱ������ʽ��������n��2ʱ����
=
=
•
��
���ܹ�֤��a1a2+a2a3+a3a4+��+anan+1��
��
| x+a-1 |
| x+2a |
| a+1 |
| x+2a |
��2����f(x)��[
| 1 |
| 2 |
| 4 |
| 5 |
|
��3������f��0��=0��a=1����f(x)=
| x |
| x+2 |
| an |
| an+2 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
����an=
| 1 |
| 2n-1 |
| 1 |
| (2n-1)•(2n+1-1) |
| 1 |
| 3 |
| 3 |
| 7 |
| 1 |
| 3 |
| 1 |
| 21 |
| 16 |
| 42 |
| 3 |
| 7 |
| anan+1 |
| an-1an |
| 2n-1-1 |
| 2n+1-2 |
| 1 |
| 2 |
| 2n-1-1 |
| 2n-1 |
| 1 |
| 2 |
| 3 |
| 7 |
����⣺��1���������У�x+2a��f��x��=x+a-1��
��x=-2a����x+a-1=-a-1=0����a=-1������a��0ì�ܣ�
��x��-2a��
��f(x)=
=1-
(x��-2a)��
��y=f��x����ͼ�������ĶԳ�ͼ�Σ���Գ�����Ϊ�㣨-2a��1����
��2����f(x)��[
��
]��
��
��
�֡�a��0����
��x��[2��3a+5]��
��3������f��0��=0��a=1��
��f(x)=
��
��0��an+1��
��
��2��
+1��
��
+1��2(
+1)��
��bn=
+1����bn+1��2bn��
�֡�an��0����bn��0����
��2��
��a1=1����b1=2��
�൱n��2ʱ��bn=b1��
��
������
��
=2n��
�֡�b1=2Ҳ����bn��2n��
��bn��2n��n��N*������
+1��2n��
��an��
(n��N*)��
Ҫʹan��
�������
ֻ��
��
����2n��11��
��n��3������������Ҫ�����С������N=3��
���ɢ�֪an=
��
��anan+1=
��
a1a2=
��
��
a1a2+a2a3=
+
=
��
��
�൱n=1��2ʱ������ʽ������
��n��2ʱ��
��
=
��
��
��anan+1��
•an-1an��(
)2•an-2an-1������(
)n-2•a2a3=
•(
)n-2��
��a1a2+a2a3+a3a4+��+anan+1��
+
(
+
+
+��+
)
=
+
(1-
)��
+
=
=
��
��x=-2a����x+a-1=-a-1=0����a=-1������a��0ì�ܣ�
��x��-2a��
��f(x)=
| x+a-1 |
| x+2a |
| a+1 |
| x+2a |
��y=f��x����ͼ�������ĶԳ�ͼ�Σ���Գ�����Ϊ�㣨-2a��1����
��2����f(x)��[
| 1 |
| 2 |
| 4 |
| 5 |
��
|
|
�֡�a��0����
|
��x��[2��3a+5]��
��3������f��0��=0��a=1��
��f(x)=
| x |
| x+2 |
��0��an+1��
| an |
| an+2 |
| 1 |
| an+1 |
| 1 |
| an |
��
| 1 |
| an+1 |
| 1 |
| an |
��bn=
| 1 |
| an |
�֡�an��0����bn��0����
| bn+1 |
| bn |
��a1=1����b1=2��
�൱n��2ʱ��bn=b1��
| b2 |
| b1 |
| b3 |
| b2 |
| bn |
| bn-1 |
| ||
| n�� |
�֡�b1=2Ҳ����bn��2n��
��bn��2n��n��N*������
| 1 |
| an |
��an��
| 1 |
| 2n-1 |
Ҫʹan��
| 1 |
| 10 |
ֻ��
| 1 |
| 2n-1 |
| 1 |
| 10 |
��n��3������������Ҫ�����С������N=3��
���ɢ�֪an=
| 1 |
| 2n-1 |
��anan+1=
| 1 |
| (2n-1)•(2n+1-1) |
a1a2=
| 1 |
| 3 |
| 3 |
| 7 |
a1a2+a2a3=
| 1 |
| 3 |
| 1 |
| 21 |
| 16 |
| 42 |
| 3 |
| 7 |
�൱n=1��2ʱ������ʽ������
��n��2ʱ��
��
| anan+1 |
| an-1an |
| 2n-1-1 |
| 2n+1-1 |
| 1 |
| 2 |
��anan+1��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 21 |
| 1 |
| 2 |
��a1a2+a2a3+a3a4+��+anan+1��
| 1 |
| 3 |
| 1 |
| 21 |
| 1 |
| 20 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
=
| 1 |
| 3 |
| 2 |
| 21 |
| 1 |
| 2n-1 |
| 1 |
| 3 |
| 2 |
| 21 |
| 18 |
| 42 |
| 3 |
| 7 |
���������⿼�����кͲ���ʽ���ۺ�Ӧ�ã��������е����ʺ�Ӧ�ã������������������������֤���������黯����ת��˼�룮�Լ���������Ҫ��Ƚϸߣ���һ����̽���ԣ��ۺ���ǿ���Ѷȴ��Ǹ߿����ص㣮����ʱҪ�������⣬��ϸ���

��ϰ��ϵ�д�
 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
�����Ŀ
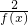 ��M��Ϊ��������
��M��Ϊ��������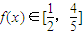 ʱ����x��ȡֵ��Χ��
ʱ����x��ȡֵ��Χ�� �����������С��N��
�������������N�� ��
��