题目内容
【题目】已知函数f(x)= ![]() x3+ax2+bx+
x3+ax2+bx+ ![]() (a,b是实数),且f′(2)=0,f(﹣1)=0.
(a,b是实数),且f′(2)=0,f(﹣1)=0.
(1)求实数a,b的值;
(2)当x∈[﹣1,t]时,求f(x)的最大值g(t)的表达式.
【答案】
(1)解:f'(x)=x2+2ax+b
∵f'(2)=0,f(﹣1)=0
∴ 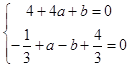 ,解得
,解得 ![]()
(2)解:由(1)可知,f(x)= ![]() ,f'(x)=x2﹣2x=x(x﹣2),
,f'(x)=x2﹣2x=x(x﹣2),
由f'(x)>0,得x<0,或x>2;由f'(x)<0,得0<x<2,
故f(x)在(﹣∞,0)和(2,+∞)单调递增,在(0,2)单调递减,
所以f(x)极小值=f(2)=0, ![]()
由 ![]() ,得x=﹣1,或x=2;
,得x=﹣1,或x=2;
由 ![]() ,得x=0,或x=3.
,得x=0,或x=3.
结合单调性及极值点,画出图像如下:
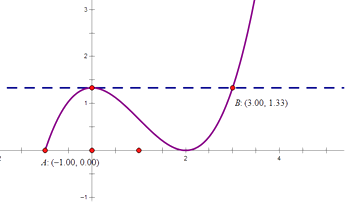
结合图像,对t分类讨论:
1)﹣1<t<0时,f(x)在[﹣1,t]上单调递增, ![]() ;
;
2)0≤t<3时, ![]() ;
;
3)t≥3时, ![]() .
.
综上可得,g(t)= 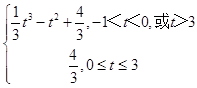
【解析】(1)直接根据f′(2)=0,f(﹣1)=0得到关于a,b的方程组,即可解出a,b的值;(2)利用导数求出f(x)的单调区间,极值点,并通过解方程f(x)= ![]() ,得到特殊点(3,
,得到特殊点(3, ![]() ),然后结合函数图像,对t分类讨论,分别求出f(x)的最大值即可.
),然后结合函数图像,对t分类讨论,分别求出f(x)的最大值即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?