题目内容
(本题满分12分)
(本题满分12分)
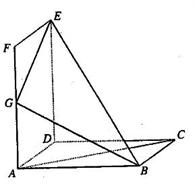
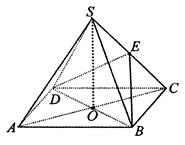
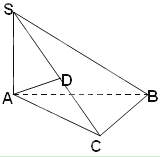
如图,已知三棱锥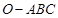 的侧棱
的侧棱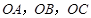 两两垂直,
两两垂直,
且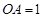 ,
, ,
,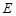 是
是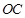 的中点。
的中点。
(1)求异面直线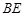 与
与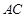 所成角的余弦值;
所成角的余弦值;
(2)求直线BE和平面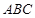 的所成角的正弦值。
的所成角的正弦值。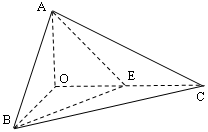
(1)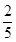 ;(2)
;(2)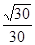 。
。
解析试题分析:(1)以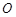 为原点,
为原点,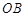 、
、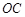 、
、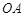 分别为
分别为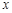 、
、 、
、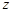 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则有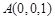 、
、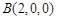 、
、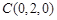 、
、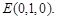 ……………………………3分
……………………………3分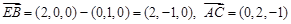
COS<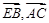 >
>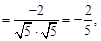 ……………………………5分
……………………………5分
所以异面直线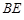 与
与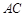 所成角的余弦为
所成角的余弦为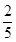 ……………………………6分
……………………………6分
(2)设平面 的法向量为
的法向量为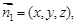 则
则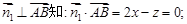
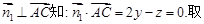
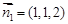 , ………8分
, ………8分
则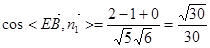 ,…………………10分
,…………………10分
故BE和平面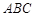 的所成角的正弦值为
的所成角的正弦值为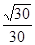 …………12分
…………12分
考点:本题考查异面直线所成的角和直线与平面所成的角。
点评:本题主要考查了空间中异面直线所成的角和直线与平面所成的角,属立体几何中的常考题型,较难.解题的关键是;首先正确的建立空间直角坐标系,然后可将异面直线所成的角转化为所对应的向量的夹角或其补角;而对于利用向量法求线面角关键是正确求解平面的一个法向量。注意计算要仔细、认真。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1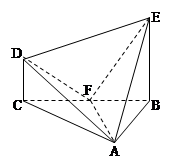
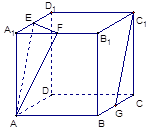
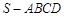 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,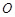 是
是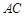 与
与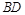 的交点,
的交点,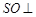 平面
平面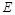 是侧棱
是侧棱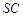 的中点,异面直线
的中点,异面直线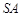 和
和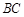 所成角的大小是60
所成角的大小是60 .
.
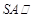 平面
平面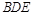 ;
;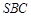 所成角的正弦值.
所成角的正弦值.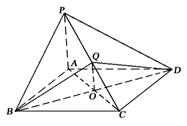
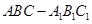 的侧面
的侧面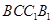 是菱形,
是菱形,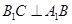 .
.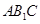
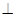 平面
平面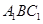 ;
;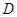 是
是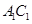 上的点,且
上的点,且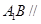 平面
平面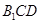 ,求
,求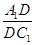 的值.
的值.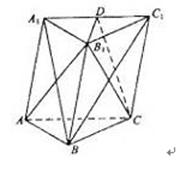
 和矩形
和矩形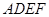 所在平面相互垂直,
所在平面相互垂直,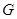 是
是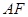 的中点.
的中点. 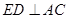 ;
;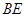 与平面
与平面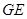 与
与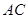 所成角的余弦值.
所成角的余弦值.