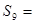题目内容
已知等差数列{an}的前n项和为Sn,且满足Sn=n2﹣n.
(1)求an;
(2)设数列{bn}满足bn+1=2bn﹣an且b1=4,
(i)证明:数列{bn﹣2n}是等比数列,并求{bn}的通项;
(ii)当n≥2时,比较bn﹣1•bn+1与bn2的大小.
(1) ;(2)(i)
;(2)(i) ,(ii)当
,(ii)当 或
或 时,
时, ,当
,当 时,
时, .
.
解析试题分析:
解题思路:(1)利用 求解即可;(2)(i)由
求解即可;(2)(i)由 构造新数列
构造新数列 ,并证明新数列为等比数列,进一步求
,并证明新数列为等比数列,进一步求 ;(ii)利用作差法判定两式的大小.
;(ii)利用作差法判定两式的大小.
规律总结:求数列的通项公式一般有三种类型:①利用等差数列、等比数列的基本量求通项公式;②已知数列的首项与递推式,求通项公式;③利用 与
与 的关系求通项公式;比较大小,往往使用作差法.
的关系求通项公式;比较大小,往往使用作差法.
试题解析:(1)当 时
时 ;当
;当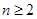 时,
时, ;
; 满足上式,
满足上式,
(2)(i)由已知得 ,即
,即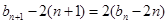 .且
.且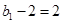 ,
,
所以数列 是以2为首项,2为公比的等比数列 ,
是以2为首项,2为公比的等比数列 ,
则 ,所以
,所以 ;
;
(ii)当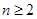 时,
时,

 ,
,
所以当 或
或 时,
时, ,当
,当 时,
时, .
.
考点:1.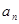 与
与 的关系;2.等比数列;3.不等式的证明.
的关系;2.等比数列;3.不等式的证明.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
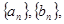
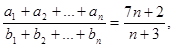 则
则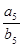 ="___________"
="___________" 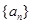 的前
的前 项和为
项和为 ,且
,且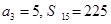 .
.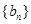 满足:
满足: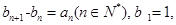 求数列
求数列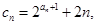 求数列
求数列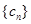 的前
的前
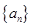 是等差数列,满足
是等差数列,满足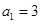 ,
,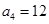 ,数列
,数列 满足
满足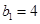 ,
,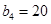 ,且
,且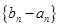 是等比数列.
是等比数列.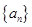 的首项
的首项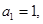 公差
公差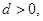 且
且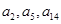 分别是等比数列
分别是等比数列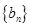 的
的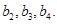
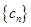 对任意正整数
对任意正整数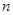 均有
均有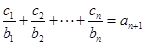 成立,求
成立,求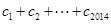 的值.
的值.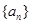 中,若
中,若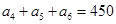 ,则
,则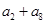 的值为 .
的值为 .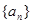 中,
中,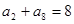 ,则该数列前9项和
,则该数列前9项和