题目内容
已知命题p:不等式|x-4|+|x-3|<m在实数集R上的解集不是空集,命题q:f(x)=-(5-2m)x是增函数,若p,q中有且仅有一个为真命题,则实数m的取值范围是 .
【答案】分析:若命题p是真命题,可求出m>1,若命题q是真命题,可求出2<m< .由题意可得m>1和2<m<
.由题意可得m>1和2<m< 中只能
中只能
有仅有一个成立,从而得到 m的取值范围.
解答:解:若命题p是真命题,由于|x-3|+|x-4|的几何意义是数轴上的点x 到3和4的距离之和,
当x在3、4之间时,这个距离和最小,是1,其它情况都大于1.
所以|x-3|+|x-4|≥1,
如果不等式|x-4|+|x-3|<m 的解集不是空集,所以 m>1.
若命题q是真命题,即f(x)=-(5-2m)x是增函数,则 0<5-2m<1,解得 2<m< .
.
由于p,q中有且仅有一个为真命题,故m>1 和2<m< 中只能有仅有一个成立,
中只能有仅有一个成立,
∴1<m≤2,或 m≥ .
.
故答案为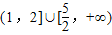 .
.
点评:本题考查绝对值不等式的几何意义,指数函数的单调性,判断m>1 和2<m< 中只能有仅有一个成立,是解题的关键,属于中档题.
中只能有仅有一个成立,是解题的关键,属于中档题.
 .由题意可得m>1和2<m<
.由题意可得m>1和2<m< 中只能
中只能有仅有一个成立,从而得到 m的取值范围.
解答:解:若命题p是真命题,由于|x-3|+|x-4|的几何意义是数轴上的点x 到3和4的距离之和,
当x在3、4之间时,这个距离和最小,是1,其它情况都大于1.
所以|x-3|+|x-4|≥1,
如果不等式|x-4|+|x-3|<m 的解集不是空集,所以 m>1.
若命题q是真命题,即f(x)=-(5-2m)x是增函数,则 0<5-2m<1,解得 2<m<
 .
.由于p,q中有且仅有一个为真命题,故m>1 和2<m<
 中只能有仅有一个成立,
中只能有仅有一个成立,∴1<m≤2,或 m≥
 .
.故答案为
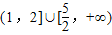 .
.点评:本题考查绝对值不等式的几何意义,指数函数的单调性,判断m>1 和2<m<
 中只能有仅有一个成立,是解题的关键,属于中档题.
中只能有仅有一个成立,是解题的关键,属于中档题. 
练习册系列答案
相关题目