题目内容
已知命题P:不等式ex>m的解集为R,命题q:f(x)=
在区间(0,+∞)上是减函数,若命题“p或q”为真,命题“p且q”为假,则实数m的取值范围是( )
| 2-m |
| x |
分析:由不等式ex>m的解集为R且指数函数的性质可知ex>0恒成立可求p;由f(x)=
在区间(0,+∞)上是减函数,结合反比例函数可求q,由p或q为真,p且q为假可知p,q一真一假
①当p真q假时,②当p假q真时,从而可求m的范围
| 2-m |
| x |
①当p真q假时,②当p假q真时,从而可求m的范围
解答:解:∵不等式ex>m的解集为R,且由指数函数的性质可知ex>0恒成立
∴P:m≤0
∵f(x)=
在区间(0,+∞)上是减函数,
∴2-m>0
q:m<2
∵“p或q”为真,命题“p且q”为假
∴p,q一真一假
①当p真q假时,则可得
,m不存在
②当p假q真时,则可得
,0<m<2
综上可得,0<m<2
故选D
∴P:m≤0
∵f(x)=
| 2-m |
| x |
∴2-m>0
q:m<2
∵“p或q”为真,命题“p且q”为假
∴p,q一真一假
①当p真q假时,则可得
|
②当p假q真时,则可得
|
综上可得,0<m<2
故选D
点评:本题主要考查了 指数函数的性质的应用,反比例函数的单调性的应用及复合命题的真假判断的应用,属于基础试题

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
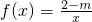 在区间(0,+∞)上是减函数,若命题“p或q”为真,命题“p且q”为假,则实数m的取值范围是
在区间(0,+∞)上是减函数,若命题“p或q”为真,命题“p且q”为假,则实数m的取值范围是