题目内容
过定点P(1,2)的直线在x轴与y轴正半轴上的截距分别为a、b,则4a2+b2的最小值为______.
解;∵过定点P(1,2)的直线在x轴与y轴正半轴上的截距分别为a、b,
把点P(1,2)代入直线的截距式方程得:
+
=1≥2
,∴ab≥8(当且仅当a=2,b=4时取等号),
又由基本不等式得:4a2+b2≥4ab(当且仅当2a=b时取等号),∴4a2+b2≥4ab≥32,(当且仅当a=2,b=4时取等号),
4a2+b2的最小值为32.
把点P(1,2)代入直线的截距式方程得:
| 1 |
| a |
| 2 |
| b |
|
又由基本不等式得:4a2+b2≥4ab(当且仅当2a=b时取等号),∴4a2+b2≥4ab≥32,(当且仅当a=2,b=4时取等号),
4a2+b2的最小值为32.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
过定点P(1,2)的直线在x轴与y轴的正半轴上的截距分别为a、b,则4a2+b2的最小值为( )
| A、8 | B、32 | C、45 | D、72 |
 轴与
轴与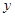 轴正半轴上的截距分别为
轴正半轴上的截距分别为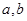 ,则
,则 的最小值为 (
)
的最小值为 (
)