题目内容
过定点P(1,2)的直线在x轴与y轴的正半轴上的截距分别为a、b,则4a2+b2的最小值为( )A.8
B.32
C.45
D.72
【答案】分析:由过定点P(1,2)的直线在x轴与y轴的正半轴上的截距分别为a、b,可得a,b的一个方程,再应用基本不等式求得4a2+b2的最小值.
解答:解:∵a>0,b>0,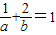
∴(2a+b)•1=(2a+b)
=2+2+
当且仅当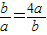 ,即2a=b=4时成立
,即2a=b=4时成立
∴2(4a2+b2)≥(2a+b)2≥64,
∴4a2+b2≥32当且仅当 时成立
时成立
∴(4a2+b2)min=32
故选B
点评:考查对于含有限制条件,应用基本不等式求最值的方法,注意“1”的代换,体现了整体思想.属中档题.
解答:解:∵a>0,b>0,
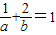
∴(2a+b)•1=(2a+b)

=2+2+

当且仅当
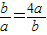 ,即2a=b=4时成立
,即2a=b=4时成立∴2(4a2+b2)≥(2a+b)2≥64,
∴4a2+b2≥32当且仅当
 时成立
时成立∴(4a2+b2)min=32
故选B
点评:考查对于含有限制条件,应用基本不等式求最值的方法,注意“1”的代换,体现了整体思想.属中档题.

练习册系列答案
相关题目
过定点P(1,2)的直线在x轴与y轴的正半轴上的截距分别为a、b,则4a2+b2的最小值为( )
| A、8 | B、32 | C、45 | D、72 |
 轴与
轴与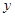 轴正半轴上的截距分别为
轴正半轴上的截距分别为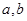 ,则
,则 的最小值为 (
)
的最小值为 (
)