题目内容

15．已知等差数列{an}的通项公式an=2n-$\frac{25}{2}$（n∈N*），则使数列{an}的前n项和Sn最小的n=6．

分析 由an=2n-$\frac{25}{2}$≤0，解得n，即可得出．

解答 解：由an=2n-$\frac{25}{2}$≤0，解得$n≤\frac{25}{4}$，
∴当n≤6时，an＜0；当n≥7时，an＞0．
∴使数列{an}的前n项和Sn最小的n=6，
故答案为：6．

点评 本题考查了等差数列的单调性、前n项和的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
14．已知定义域为（2a，1-a）的函数f（x）=lg（$\sqrt{{x}^{2}+b}$+ax）是奇函数，则b=1．
6．直线ax-y+3=0与圆（x-1）2+（y-2）2=4相交于A、B两点且|AB|=2$\sqrt{3}$，则a的值为（　　）
A．3B．2C．1D．0
3．设函数f（x）=$\left\{\begin{array}{l}{x-[x]，x≤0}\\{f（x-1），x＞0}\end{array}\right.$，其中[x]表示不超过x的最大整数，如：[-1，2]=-2，[1，2]=1，[1]=1．则（i）f（3.15）=0.15； （ii）若关于x的方程f（x）=kx+k有三个不同的根，则实数k的取值范围是$\frac{1}{4}$≤k＜$\frac{1}{3}$或-1＜k≤-$\frac{1}{2}$．
10．设函数f（x）=x2+c，若${∫}_{0}^{1}$f（x）dx=1，则c=$\frac{2}{3}$．
20．函数f（x）=sinx+cosx图象的一个对称轴方程是（　　）
A．x=πB．x=$\frac{π}{4}$C．x=$\frac{π}{2}$D．x=$\frac{π}{8}$
7．将函数y=f（x）的图象上的每一点的纵坐标扩大到原来的4倍，横坐标扩大到原来的2倍，若把所得的图象沿x轴向左平移$\frac{π}{2}$个单位后得到的曲线与y=2sinx的图象相同，则函数y=f（x）的解析式为（　　）
A．y=-$\frac{1}{2}$cos2xB．y=$\frac{1}{2}$cos2xC．y=-$\frac{1}{2}$sin2xD．y=$\frac{1}{2}$sin2x
4．已知函数$f（x）=\frac{{{x^2}+1}}{bx+c}$是奇函数，且f（1）=2，
（1）求f（x）的解析式；
（2）判断函数f（x）在[1，+∞）上的单调性；
（3）求函数在区间[1，3]上的最大、小值．
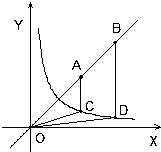5．如图，点A、B为直线y=x上的两点，过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$（x＞0）于C、D两点．若BD=2AC，则4OC2-OD2的值为6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网