题目内容
平面直角坐标系中,如果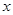 与
与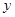 都是整数,就称点
都是整数,就称点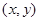 为整点,命题:
为整点,命题:
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②如果 与
与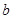 都是无理数,则直线
都是无理数,则直线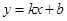 不经过任何整点;
不经过任何整点;
③如果 与
与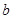 都是有理数,则直线
都是有理数,则直线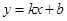 必经过无穷多个整点;
必经过无穷多个整点;
④如果直线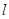 经过两个不同的整点,则
经过两个不同的整点,则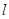 必经过无穷多个整点;
必经过无穷多个整点;
⑤存在恰经过一个整点的直线;
其中的真命题是 (写出所有真命题编号).
①④⑤
解析试题分析:不与坐标轴平行的直线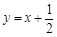 中横坐标为整数时,纵坐标为分数,同理纵坐标为整数时,横坐标为分数,即不经过任何整点,所以①正确,③不正确. 直线
中横坐标为整数时,纵坐标为分数,同理纵坐标为整数时,横坐标为分数,即不经过任何整点,所以①正确,③不正确. 直线 中
中 与
与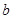 都是无理数,但经过唯一一个整数点
都是无理数,但经过唯一一个整数点 所以②不正确,⑤正确.设直线
所以②不正确,⑤正确.设直线 经过整数点
经过整数点 则直线
则直线 必经过点
必经过点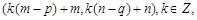 由于
由于 不同时成立,所以点
不同时成立,所以点 有无数个.
有无数个.
考点:直线整点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点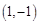 到直线
到直线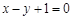 的距离是 ( ▲ )
的距离是 ( ▲ )
A.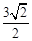 | B.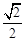 | C.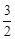 | D.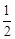 |
 ,且与直线
,且与直线 垂直的直线方程是 .
垂直的直线方程是 .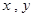 满足等式
满足等式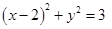 ,那么
,那么 的最大值为______.
的最大值为______.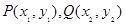 之间的“直角距离”为
之间的“直角距离”为 .现有下列命题:
.现有下列命题: ) (
) ( ),则d(P,Q)为定值;
),则d(P,Q)为定值;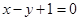 上任一点P的直角距离d (O, P)的最小值为
上任一点P的直角距离d (O, P)的最小值为 ;
;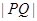 表示P、Q两点间的距离,那么
表示P、Q两点间的距离,那么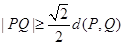 ;
;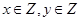 ,若点A是在过P (1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.
,若点A是在过P (1,3)与Q(5,7)的直线上,且点A到点P与Q的“直角距离”之和等于8,那么满足条件的点A只有5个.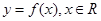 ,对函数
,对函数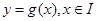 ,定义
,定义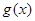 关于
关于 的对称函数为函数
的对称函数为函数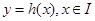 ,
,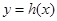 满足:对于任意
满足:对于任意 ,两个点
,两个点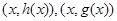 关于点
关于点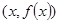 对称,若
对称,若 是
是 关于
关于 的“对称函数”,且
的“对称函数”,且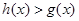 恒成立,则实数
恒成立,则实数 的取值范围是_________.
的取值范围是_________.