Question

【题目】某高校在2012年的自主招生考试成绩中随机抽取100名中学生的笔试成绩，按成绩分组，得到的频率分布表如下所示.

组号	分组	频数	频率
第1组	[160,165)	5	0.050
第2组	[165,170)	①	0.350
第3组	[170,175)	30	②
第4组	[175,180)	20	0.200
第5组	[180,185)	10	0.100
合计	100	1.00

（1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图，并从频率分布直方图中求出中位数（中位数保留整数）；

（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，从这6名学生中随机抽取2名学生接受A考官进行面试，求：第4组至少有一名学生被考官A面试的概率．

Answer 1

【答案】（1）见解析,中位数172；（2）.

【解析】

（1）由频率分布直方图能求出第2组的频数，第3组的频率，从而完成频率分布直方图．

（2）设第3组的3位同学为A1，A2，A3，第4组的2位同学为B1，B2，第5组的1位同学为C1，利用列举法能出从这六位同学中抽取两位同学，第4组至少有一名学生被考官A面试的概率．

(1)①由题可知，第2组的频数为0.35×100＝35人，②第3组的频率为＝0.300，

频率分布直方图如图所示，

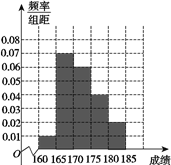
160至165的频率为0.05，165至170的频率为0.35，170至175的频率为0.30

故知中位数在170至175之间，设为x，

则（x﹣170）×0.06+0.40＝0.5，

解得x＝172，故中位数为172．

(2)因为第3、4、5组共有60名学生，所以利用分层抽样在60名学生中抽取6名学生进入第二轮面试，每组抽取的人数分别为：

第3组：×6＝3人，

第4组：×6＝2人，

第5组：×6＝1人，

所以第3、4、5组分别抽取3人、2人、1人进入第二轮面试．

设第3组的3位同学为A1，A2，A3，第4组的2位同学为B1，B2，第5组的1位同学为C1，

则从这六位同学中抽取两位同学有

(A1，A2)，(A1，A3)，(A1，B1)，(A1，B2)，(A1，C1)，(A2，A3)，(A2，B1)，(A2，B2)，(A2，C1)，(A3，B1)，(A3，B2)，(A3，C1)，(B1，B2)，(B1，C1)，(B2，C1)，共15种，

其中第4组的2位同学B1，B2中至少有一位同学入选的有：(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)，(B1，C1)，(B2，C1)，共有9种，所以第4组至少有一名学生被考官A面试的概率为.