题目内容
9. 如图,在四棱锥 A-BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4.
如图,在四棱锥 A-BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4.(1)求证:平面 ADE⊥平面BCD;
(2)求证:FB∥平面ADE;
(3)求四棱锥A-BCDE的体积.
分析 (1)利用等边三角形的性质可得AM⊥DE,在△DMC中,利用余弦定理可得MC2=13,利用勾股定理的逆定理可得:AM⊥MC,再利用线面垂直与面面垂直的判定定理即可证明.
(2)分别取AD,DC的中点G,N,连接FG,GE,FN,NB.利用三角形中位线定理与平行四边形的性质可得:$FG\underset{∥}{=}DN$,可得△BCN是等边三角形,可得四边形EBND是平行四边形,$DN\underset{∥}{=}EB$,$FB\underset{∥}{=}GE$,可得FB∥平面ADE;
(3)过点B作BH⊥NC于点H,可得BH.又EB=ND=2,利用四棱锥A-BCDE的体积V=$\frac{1}{3}{S}_{四边形EBCD}×AM$,即可得出.
解答 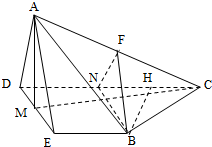 (1)证明:∵△AD E是等边三角形,M是D E的中点,
(1)证明:∵△AD E是等边三角形,M是D E的中点,
∴AM⊥DE,${A}{M}=\sqrt{3}$,
∵在△DMC中,DM=1,∠CDM=60°,CD=4,
∴MC2=42+12-2×4×1×cos60°=13,
∴${M}C=\sqrt{13}$,
∵在△AMC中,A M2+MC2=3+13=16=AC2,
∴AM⊥MC,
∵MC∩DE=M,MC?平面BCD,DE?平面BCD,
∴AM⊥平面BCD,
∵AM?平面ADE,
∴平面ADE⊥平面BCD.
(2)证明:分别取AD,DC的中点G,N,连接FG,GE,FN,NB.
∵AC=DC,F,NF分别为AC,DC的中点,
∴$FN\underset{∥}{=}\frac{1}{2}AD$,∴$FN\underset{∥}{=}GD$,
∴FN$\underset{∥}{=}$DN,
∴四边形DNFG是平行四边形,
∴$FG\underset{∥}{=}DN$,
∵点N是DC的中点,
∴BC=NC,又∠BCN=60°,
∴△BCN是等边三角形,
∴∠CNB=∠CDE=60°,
∴$BN\underset{∥}{=}DE$,
∴四边形EBND是平行四边形,
∴$DN\underset{∥}{=}EB$,
∴$FB\underset{∥}{=}GE$,
又?平面ADE,GE?平面ADE,
∴FB∥平面ADE;
(3)解:过点B作BH⊥NC于点H,则BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.
由(2)可知:四边形EBND是平行四边形,
∴EB=ND=2,
∴底面等腰梯形BCDE的面积S四边形EBCD=$\frac{1}{2}×(2+4)×\sqrt{3}$=3$\sqrt{3}$,
∴四棱锥A-BCDE的体积V=$\frac{1}{3}{S}_{四边形EBCD}×AM$=$\frac{1}{3}×3\sqrt{3}×\sqrt{3}$=3.
点评 本题考查了等腰梯形与平行四边形的性质、线面面面平行垂直的判定与性质定理、四棱锥的体积计算公式、三角形中位线定理,考查了推理能力与计算能力,属于中档题.

| A. | {x|-2≤x≤1} | B. | {x|0<x≤1} | C. | {x|-1≤x≤1} | D. | {x|x<1} |
 某工厂为了检查一条流水线的生产情况,从该流水线上随机抽取40件产品,测量这些产品的重量(单位:克),整理后得到如下的频率分布直方图(其中重量的分组区间分别为(490,495],(495,500],(500,505],(505,510],(510,515])
某工厂为了检查一条流水线的生产情况,从该流水线上随机抽取40件产品,测量这些产品的重量(单位:克),整理后得到如下的频率分布直方图(其中重量的分组区间分别为(490,495],(495,500],(500,505],(505,510],(510,515])
 如图,△ABC中,AC=BC=$\frac{\sqrt{2}}{2}$AB,四边形ABED是边长为a的正方形,平面ABED⊥平面ABC,若G、F分别是EC、BD的中点.
如图,△ABC中,AC=BC=$\frac{\sqrt{2}}{2}$AB,四边形ABED是边长为a的正方形,平面ABED⊥平面ABC,若G、F分别是EC、BD的中点.