题目内容
1.如图(1),矩形ABCD中,AB=2AD,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE.且在射线CE上取一点M,使EM=AB,如图(2),求证:DE⊥平面ADM.
分析 取AE的中点F,连接DF,BF,设AD=1,求出BD,由勾股定理可证DE⊥BE,由EM=AB且,EM∥AB,可证DE⊥MA,又由已知可得DE⊥AD,MA∩AD=A,即可证明DE⊥平面MDA.
解答 证明: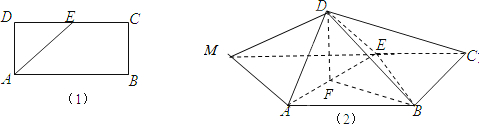 如图(2),取AE的中点F,连接DF,BF,设AD=1,
如图(2),取AE的中点F,连接DF,BF,设AD=1,
∵AD=DE=1,∴DF⊥AE,由AD⊥DE,可得AE=$\sqrt{2}$,AF=$\frac{\sqrt{2}}{2}$,DF=$\sqrt{D{A}^{2}-A{F}^{2}}$=$\frac{\sqrt{2}}{2}$,
∵平面ADE⊥平面ABCE.
∴DF⊥BF,
∵AB=2,AE=$\sqrt{2}$,BE=$\sqrt{B{C}^{2}+E{C}^{2}}$=$\sqrt{2}$,
∴由勾股定理可得:∠BEF=90°,
∴BF=$\sqrt{B{E}^{2}+E{F}^{2}}$=$\sqrt{\frac{5}{2}}$,
∴DB=$\sqrt{D{F}^{2}+B{F}^{2}}$=$\sqrt{3}$,
∵DE=1,BE=$\sqrt{2}$.
∴由勾股定理可得:∠BED=90°,即DE⊥BE,
∵EM=AB且,EM∥AB,∴MA∥BE,
∴DE⊥MA,
又由已知可得DE⊥AD,MA∩AD=A,
∴DE⊥平面MDA.
点评 本题主要考查了直线与平面垂直,折叠问题,考查空间想象能力,计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
13.已知集合A={1,2},B={x|x-1|≤1},则A∩B等于( )
| A. | {-2} | B. | {1,2} | C. | {1} | D. | {-1,1,2} |
16.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为( )
| A. | $\frac{1}{6}$a3 | B. | $\frac{{\sqrt{2}}}{12}$a3 | C. | $\frac{{\sqrt{3}}}{12}$a3 | D. | $\frac{{\sqrt{3}}}{6}$a3 |
6.已知f(x)=lnx-$\frac{x}{4}$+$\frac{3}{4x}$,g(x)=-x2-2ax+4,若对?x1∈(0,2],?x2∈[1,2],使得f(x1)≥g(x2)成立,则a的取值范围是( )
| A. | [-$\frac{1}{8}$,+∞) | B. | [$\frac{25-8ln2}{16}$,+∞) | C. | [-$\frac{1}{8}$,$\frac{5}{4}$] | D. | (-∞,$\frac{5}{4}$] |
10.执行如图的程序框图,若输入的a=209,b=76,则输出的a是( )


| A. | 3 | B. | 57 | C. | 19 | D. | 76 |
 如图,在四棱锥 A-BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4.
如图,在四棱锥 A-BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4.