题目内容
设函数 的定义域为
的定义域为 ,当
,当 时,
时,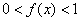 ,
,
且对于任意的实数 、
、 ,都有
,都有 .
.
(1)求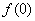 ;
;
(2)试判断函数 在
在 上是否存在最小值,若存在,求该最小值;若不存在,说明理由;
上是否存在最小值,若存在,求该最小值;若不存在,说明理由;
(3)设数列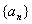 各项都是正数,且满足
各项都是正数,且满足 ,
, (
( ),又设
),又设 ,
, ,
,
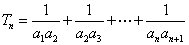 , 当
, 当 时,试比较
时,试比较 与
与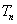 的大小,并说明理由.
的大小,并说明理由.
【答案】
(1)令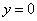 ,
, 得
得 ,又
,又 ∴
∴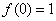
(2)∵ 时,
时,
∴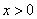 时,
时,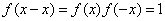 得
得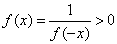 ,
,
故对于 ,
,
任取实数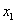 ,
,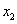 ,且
,且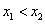 ,则
,则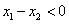 ∴
∴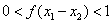
∴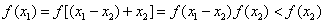
∴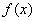 在
在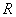 上为增函数
上为增函数
∴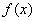 在
在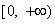 上存在最小值,
上存在最小值, ;
;
(3)由 得
得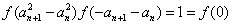
即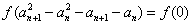 ,又
,又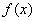 在
在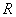 上为增函数
上为增函数
∴
∴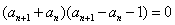 ,又数列
,又数列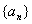 各项都是正数
各项都是正数
∴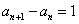 ,
,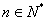
∴数列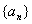 为等差数列,
为等差数列,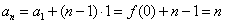
∵ ,∴
,∴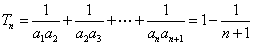
而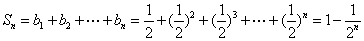
当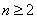 时,
时,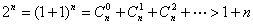 ,
,
故 ∴
∴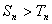
综上,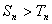 (
(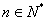 且
且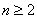 )
)

练习册系列答案
相关题目
 ,求实数
,求实数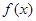 的定义域为
的定义域为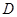 ,若存在非零常数
,若存在非零常数 使得对于任意
使得对于任意 有
有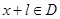 且
且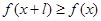 ,则称
,则称 上的
上的 的奇函数
的奇函数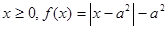 ,若
,若 的取值范围为________.
的取值范围为________.