题目内容
设函数![]() 的定义域为R, 当x<0时,
的定义域为R, 当x<0时, ![]() >1, 且对于任意的实数
>1, 且对于任意的实数![]() , 有
, 有
![]() 成立. 又数列
成立. 又数列![]() 满足
满足![]() , 且
, 且![]()
(1)求证: ![]() 是R上的减函数;
是R上的减函数;
(2)求![]() 的值;
的值;
(3)若不等式![]() ≥k ?
≥k ?![]() 对一切
对一切![]() 均成立, 求
均成立, 求![]() 的最大值.
的最大值.
解析: (1)由题设, 令x= -1, y=0, 可得f(-1)=f(-1)f(0), ∴ f(0)=1. 故a1=f(0)=1
当x>0时, -x<0, ∴ f(-x)>1, 且 1=f(0)=f(x)f(-x), 故得 0<f(x)<1
从而可得f(x)>0, x∈R
设x1, x2∈R, 且x1<x2, 则x2-x1>0, 故f(x2-x1)<1, f(x1)>0
从而f(x1) -f(x2)=f(x1) -f(x1+x2-x1)=f(x1) -f(x1)f(x2-x1)=f(x1)[1-f(x2-x1)]>0
即f(x1)>f(x2), ∴函数f(x)在R上是减函数.
(2)由f(an+1)=![]() , 得f(an+1)f( -2-an)=1, 即f(an+1-an-2)=f(0)
, 得f(an+1)f( -2-an)=1, 即f(an+1-an-2)=f(0)
由f(x)的单调性, 故an+1-an-2=0 即an+1-an=2 (n∈N*)
因此, {an}是首项是1, 公差为2的等差数列, 从而an=2n-1, ∴ a2007=4013
(3)设g(n)=![]() , 则g(n)>0, 且k≤g(n)对n∈N*恒成立.
, 则g(n)>0, 且k≤g(n)对n∈N*恒成立.
由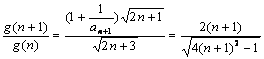 >1, 即g(n+1)>g(n),
>1, 即g(n+1)>g(n),
∴ g(n)在N*上为单调递增函数, 故g(n)≥g(1)=![]()
![]()
因此, k≤![]()
![]() , 即k的最大值为
, 即k的最大值为![]()
![]()

练习册系列答案
相关题目
设函数 的定义域为R+,若对于给定的正数K,定义函数
的定义域为R+,若对于给定的正数K,定义函数 ,则当函数
,则当函数 时,定积分
时,定积分 的值为
的值为
( )
| A.2ln2+2 | B.2ln2-1 | C.2ln2 | D.2ln2+1 |
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
 的值;
的值; 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值. 的定义域为R,如果存在函数
的定义域为R,如果存在函数 为常数),使得
为常数),使得 对于一切实数
对于一切实数 都成立,那么称
都成立,那么称 为函数
为函数 ,
, 是函数
是函数 的一个承托函数,记实数a的取值范围为集合M,则有( )A.
的一个承托函数,记实数a的取值范围为集合M,则有( )A. 



 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 ,
, ,有
,有
 ; (2)试判断函数
; (2)试判断函数 在
在 上是否存在最大值,若存在,求出该最大值,若不存在说明理由;
上是否存在最大值,若存在,求出该最大值,若不存在说明理由; 各项都是正数,且满足
各项都是正数,且满足
 ,又设
,又设 ,
, ,试比较
,试比较 与
与  的大小.
的大小.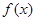 的定义域为R,且
的定义域为R,且

 的取值范围是 ( )
的取值范围是 ( )  B.(
B.(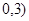 C.(
C.( D.
D.