题目内容
【题目】已知函数![]() 的图象过原点,且在原点处的切线与直线
的图象过原点,且在原点处的切线与直线![]() 垂直.
垂直.![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论![]() 的单调性;
的单调性;
(2)若对任意的![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)分类讨论,详见解析;(2)![]() .
.
【解析】
(1)首先由题可得![]() ,由此得到
,由此得到![]() ,再分
,再分![]() ,
,![]() 及
及![]() 讨论得出结论;
讨论得出结论;
(2)所求问题等价于![]() 在
在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,只需求出函数
,只需求出函数![]() 在
在![]() 上的最大值即可.
上的最大值即可.
(1)依题意,![]() ,即
,即![]() ,故
,故![]() ,
,
由在原点处的切线与直线![]() 垂直可知,
垂直可知,![]() ,则
,则![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上恒成立,此时函数
上恒成立,此时函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() 解得
解得![]() 或
或![]() ,由
,由![]() 解得
解得![]() ,
,
此时函数![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
③当![]() 时,由
时,由![]() 解得
解得![]() 或
或![]() ,
,![]() 解得
解得![]() ,
,
此时函数![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)由(1)可知,![]() ,则
,则![]() 对任意
对任意![]() 上恒成立,
上恒成立,
![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
由![]() 解得
解得![]() ,
,
易知当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
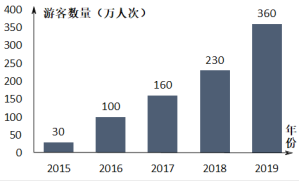
启东小题作业本系列答案【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: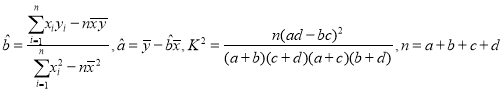 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
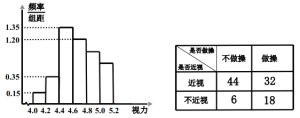
【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.
(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.
附: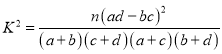
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着![]() 三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择
三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择![]() 三个项目的意向如下:
三个项目的意向如下:
扶贫项目 |
|
|
|
贫困户 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每个贫困户只能从自己已登记的选择意向中随机选取一项,且每个项目至多有两个贫困户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.为了比较注射A,B两种疫苗后产生的抗体情况,选200只小鼠做实验,将这200只小鼠随机分成两组,每组100只,其中一组注射疫苗A,另一组注射疫苗B.下表1和表2分别是注射疫苗A和疫苗B后的实验结果.
表1:注射疫苗A后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射疫苗B后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
(1)完成下面频率分布直方图,并比较注射两种疫苗后抗体参数的中位数大小;
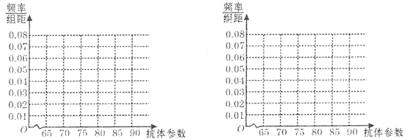
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B后的抗体参数有差异”.
表3:
抗体参数小于75 | 抗体参数不小于75 | 合计 | |
注射疫苗A | a= | b= | |
注射疫苗B | c= | d= | |
合计 | n= |
附: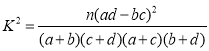
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 10.828 |