题目内容
【题目】某个服装店经营某种服装，在某周内获纯利y(元)与该周每天销售这些服装件数x之间有如下一组数据：
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知
＝280， 
yi＝3 487，
(1)求
；
(2)求纯利y与每天销售件数x之间的回归直线方程；
(3)每天多销售1件，纯利y增加多少元？
【答案】（1）6,79.86；（2）
＝51.36＋4.75x，（3）每天多销售1件，纯利平均增加4.75元．
【解析】试题分析：（1）根据平均数的公式，即可求得
的值；
（2）利用回归系数的计算公式，求解
，代入
，求得
，即可得到回归方程；
（3）利用回归直线方程，即可作出每天多销售1件，纯利平均增加值，作出预测．
试题解析：
(1)
＝
(3＋4＋5＋…＋9)＝6，
＝ (66＋69＋…＋91)≈79.86.
(2)设回归直线方程为
＝
＋
x，
则＝
＝
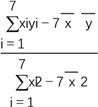≈4.75.
＝－≈79.86－4.75×6＝51.36.
∴所求的回归直线方程为＝51.36＋4.75x.
（3）每天多销售1件，纯利平均增加4.75元．
练习册系列答案
相关题目
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据，根据表提供的数据，求出y关于x的线性回归方程为 
=0.7x+0.35，则下列结论错误的是（ ）
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点（4，5，3，5）
D.A产品每多生产1吨，则相应的生产能耗约增加0.7吨
